前回、台形積分法に言いがかりをつけるにあたって、勢いで、
「台形積分法はL安定」ではない、とやったんですが、L安定とは、
「A安定でかつ、\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty}x_{i}=0\)」ですよね。\( Re(\lambda)\rightarrow-\infty\)なんて固有値を問題にしていいんでしょうか?虚軸方向は「Nyquist 周波数を超えたら意味はない」とブチかましておいて。
やはり、実数軸方向にも頃合いってもんがあるのでは?
ということで、前回の図4を再掲します。
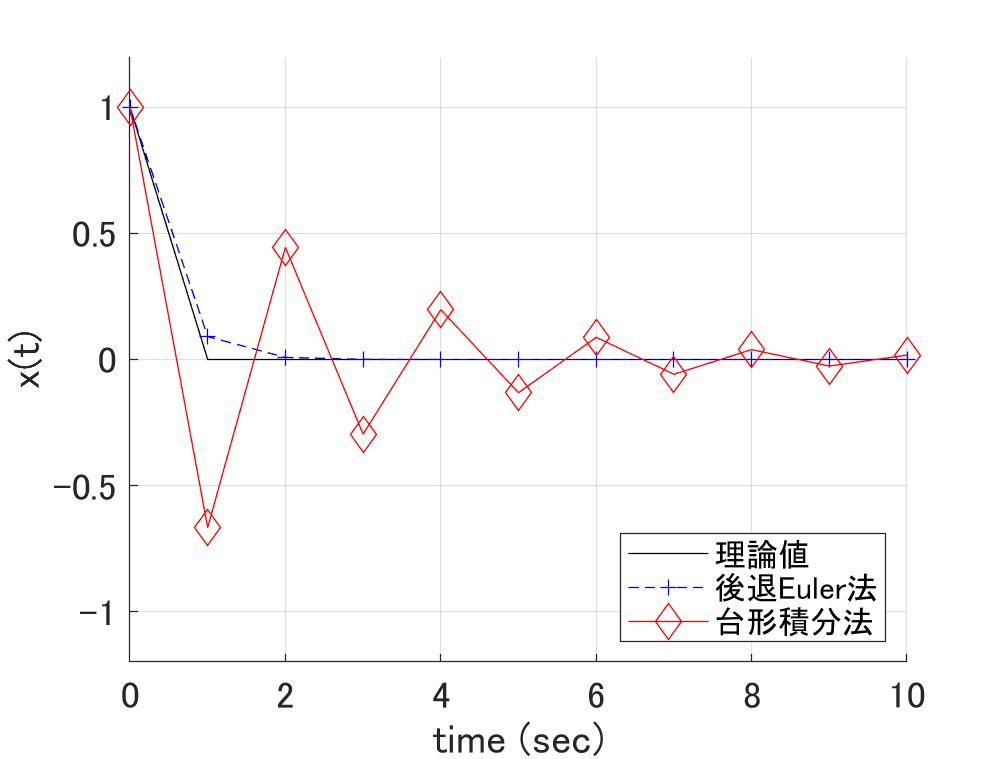
図1a \(h\lambda=-10\) 図1b \(h\lambda=-100\)
計算しているのは、
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \qquad x(0)=1
\label{eq:Test}
\end{equation}
なので、ズバリ、
\begin{equation}
x(t) = e^{\lambda t}
\label{eq:AnSolution}
\end{equation}
が解析解ですが、例によって\(h=1\)で計算した場合、最初の1ステップ\((t=1)\)の値は
\(\lambda=-10\)の場合、\(e^{-10}=0.000045\)、
\(\lambda=-100\)の場合、\(e^{-100}=3.7201×10^{-44}\)
です。
ゼロの数を数えてくださいよ。計算初日(最初の1ステップ)で限りなくゼロです。過渡特性もなにもあったもんじゃない。
こんな固有値、計算する必要があるでしょうか?
という事で、実軸の固有値の限界を探ってみると、
\(h\lambda=-3\)の場合、\(e^{-3}=0.0498\)
\(h\lambda=-4\)の場合、\(e^{-4}=0.0183\)
\(h\lambda=-5\)の場合、\(e^{-5}=0.0067\)
\(h\lambda=-5\)までいけば、0.67%なので十分、2ステップ目からはさらにゼロに近づくことを考慮すれば、\(h\lambda=-4\)、\(h\lambda=-3\)でも大丈夫でしょう。

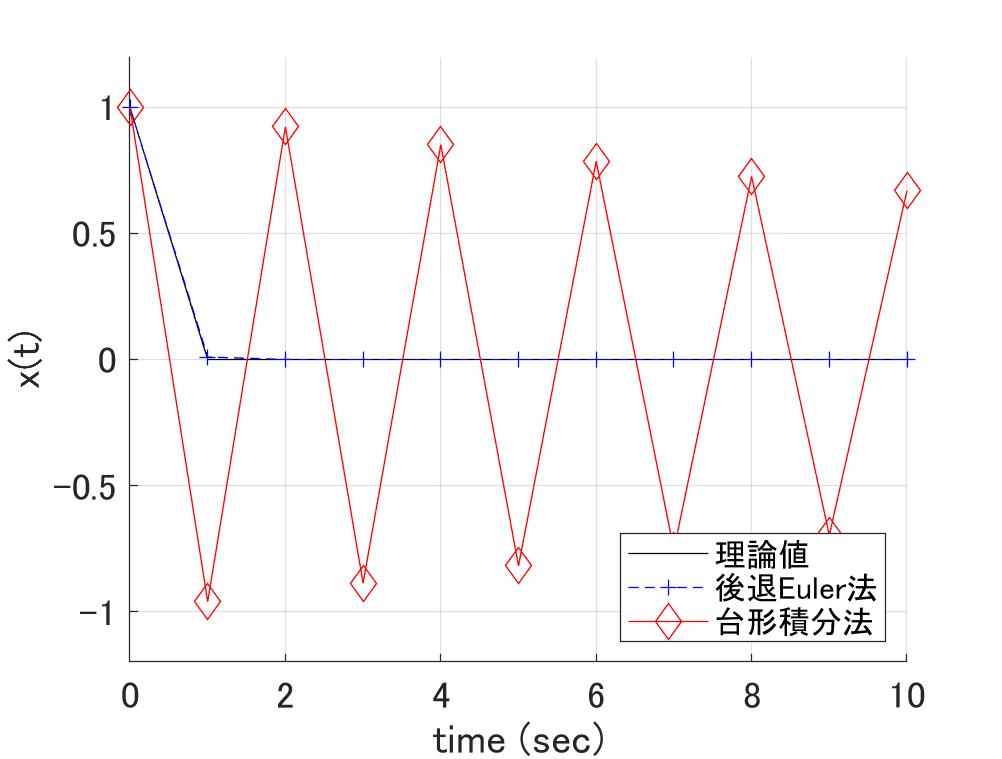
図2 \(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果
という事で、Stiffな方程式を計算するときに必要な安定領域は、虚数軸方向はNyquist 周波数ということで±3.14i、実数軸方向は-3の図3の領域で十分であり、必ずしもA安定である必要はない[1] … Continue reading、というのが結論です。
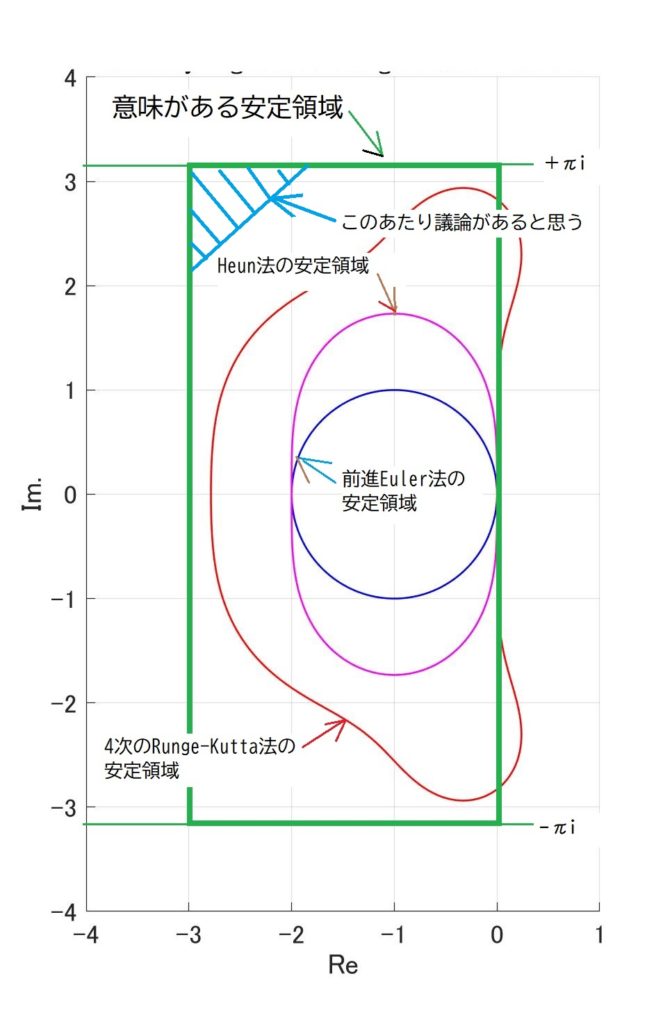
図3 意味があると考える安定領域
「ですがね。計算しろよ!って渡された方程式が、都合の良い固有値を持ってる保証はないんですぜ、ダンナ」と数値解法君はおっしゃるでしょうね。
「しかしだ君。先ずは、安定領域内であれば、まともな精度で計算をやってあげるのが、君の誠というものではないかね、数値解法君?」
「安定であればどこでも、まともな計算精度」は少々厳しいので、まちの制御屋が意味があると断定した、実軸方向で\([-3,0]\)、虚軸方向で\([-\pi i,+\pi i]\)の範囲を安定領域に含み、この領域でまともな精度を持つ数値解法が欲しいところです。
4次のRunge-Kutta法は、残念ながら安定領域が足りません。陰解法に頼ろうにも、\(1<|h\lambda|\)の条件では、後退Euler法や台形積分法は適合次数が低く、Taylor級数の打ち切った項のタタリが怖すぎます[2]虚軸方向で考察した、Taylor展開の収束の遅さは実軸でも同様。
これらを凌ぐ、安定領域が広く精度の高い手法はあるのでしょうか?
次回です。
参考文献
1: 「常微分方程式の数値解法 Ⅱ」 E. ハイラー G、ヴァンナー 三井 斌友 監訳
2008年 シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー,L.R.ペツォルド,
中村 眞理雄 監訳 嘉村友作・三ツ間 均 共訳 2006年 培風館