月: 2021年6月

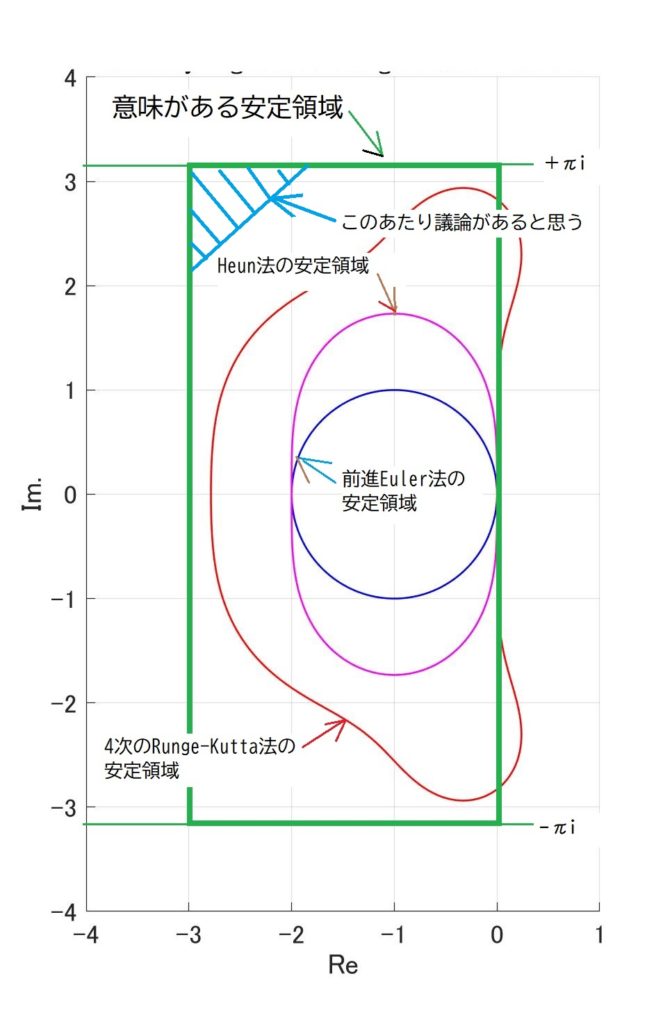
前回、必要な安定領域は実軸方向で\([-3,0]\)、虚軸方向で\([-\pi i,+\pi i]\)の範囲と勝手に決めつけたわけですが、この領域で安定でまともな計算精度がある数値解法はあるのでしょうか？
いずれじっくりやりたいと思いますが、こういう場合の定番の後退微分法（BDF）やAdams-Moulton法が候補に入らなことは事は図1^[1]いずれじっくりやりますので、図が甘いのはご容赦くださいで示しておきます。
後退微分法（Gear法とも言う）は3段^[2]Wikipediaの訳に従い”段”としましたが、英語ではStepです。Runge-Kutta法のときは、Stageを段と訳しているので、非常に紛らわしいの場合は（緑の線）と虚軸がわずかに安定領域から外れ、4段になるとオイシイ領域が不安定になり、6段を超えると不安定という、実はけっこう痛い奴です^[3]Stiff-Solverの代表格である後退微分法は3次以上はA安定じゃない、というのが衝撃の事実。

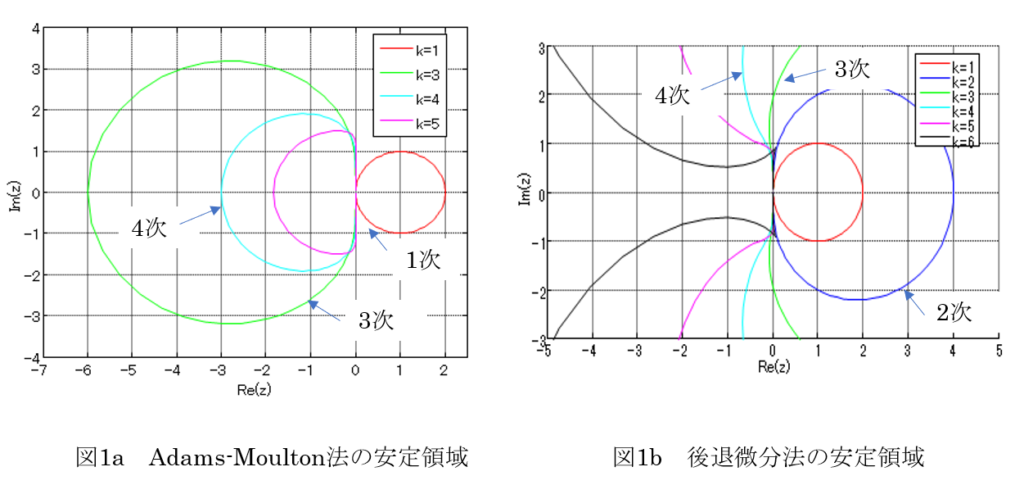
おや、台形積分も、後退Eulerも、Adams-Moultonも、Gearも、全部だめなら、候補は残るのか？

それがあります。線形式に限定すれば、ありえます。

最初の「常微分方程式と状態方程式」で書きましたが、線形の常微分方程式である状態方程式
\begin{equation}
\frac{dX(t)}{dt}=AX(t)+BU(t)
\label {eq:StateEq_9}
\end{equation}
の場合、\(X_i=X(t_0)、　X_{i+1}=X(h+t_0)\)とすれば、
\begin{equation}
X_{i+1}=e^{A h}X_i + (e^{A h} – I )A^{-1} BU_i
\label{eq:diffExp_9}
\end{equation}
となるので式\eqref{eq:diffExp_9}を計算すれば、\(X_iからX_{i+1}\)が即座に得られますよね、と。

ですが、行列指数関数\(e^{A}\)は、
\begin{equation}
e^{A}:=I+A+\frac{A^2}{2!}+…+\frac{A^N}{N!}= \sum_{k=0}^{N} \frac{A^k}{k!}
\label{eq:defMatExp_9}
\end{equation}
において\(N\rightarrow\infty\)なんですが、これはどうやって計算するのでしょうか？
式\eqref{eq:defMatExp_9}をそもまま頑張って計算する？　\(N=\infty\)まで？

たしかに、\(\infty\)まではできませんが、この手の式の高次項は収束するのがお約束なので適当なところまで頑張ればOK、のはずです。適当なところまで頑張ってみましょう。

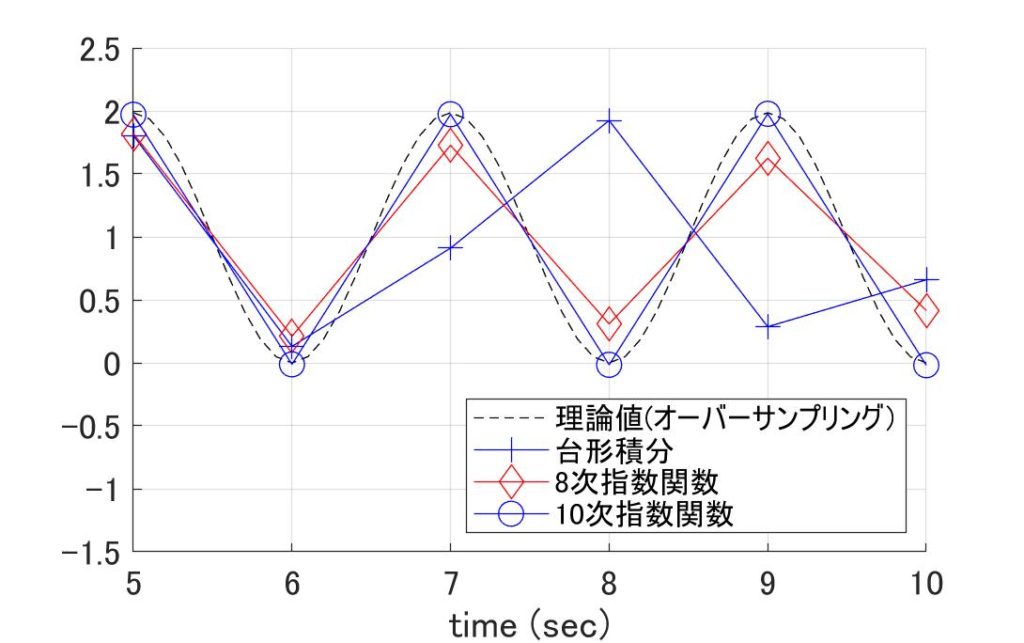
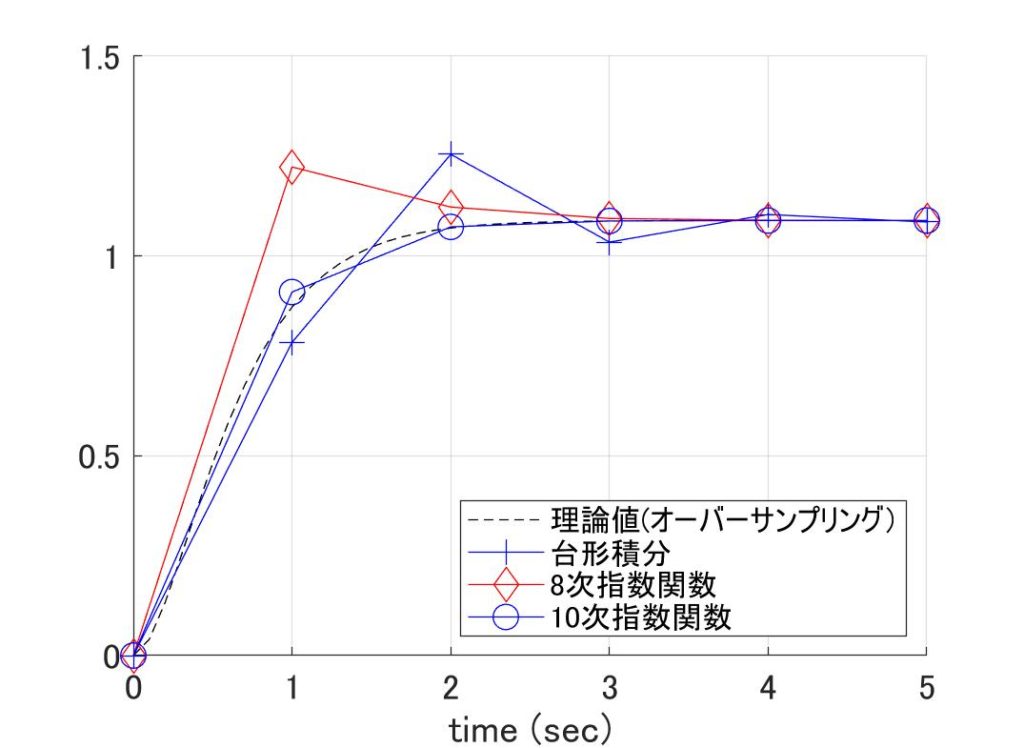
しかし、「台形積分法に言いがかりをつける」でも書きましたが、\(h\lambda=3\)の場合\(( 3^k/k! )\)が１より小さくなるのは\(k=7\)の時です。従って、少なくとも\(N=7\)を超えないとマズそうなので、イロを付けて\(N=10\)まで頑張ってみたのが図2です。

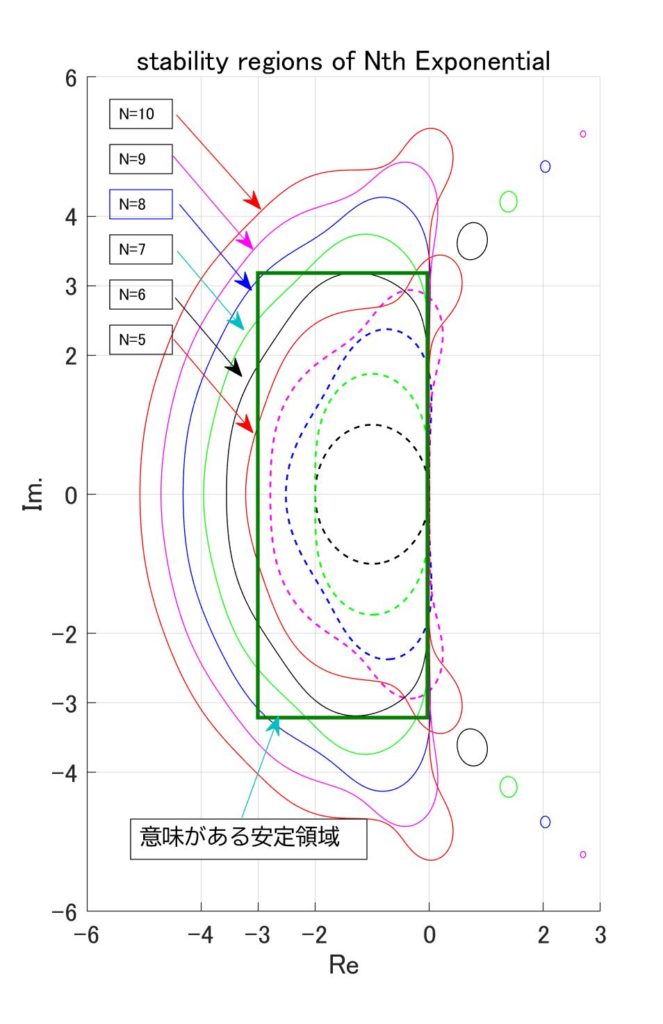
図2　N次で打ち切った指数関数の安定領域

式\eqref{eq:defMatExp_9}の行列指数関数を\(N\)次で打ち切ったものを使用して、式\eqref{eq:diffExp_9}を計算した場合の安定領域は、実はRunge-Kutta法と同じ^[4]「Taylor展開とRunge-Kutta法」の時にやりましたなので、4次まではよく見かけると思いますが、5次から先は初めて見たのではないでしょうか？
まちの制御屋もこの図2が出てくる論文^[5]”On the absolute stability regions corresponding to partial sums of the exponential function” D.Ketchenson et al. IMA Journal of Numerical Analysis, Volume 35, Issue 3, July 2015, Pages … Continue readingを見つけたときは、胸が張り裂けそうでした。

式\eqref{eq:diffExp_9}は厳密解なので、\(N=\infty\)まで頑張ればA安定のはずですが、たかだか\(N=10\)程度では、安定領域はかなり小さいです。ですが\(N=8\)を超えれば、まちの制御屋が意味のある安定領域とした領域を含みます。さらに\(N=10\)であれば^[6] … Continue reading、計算精度は\(h^{10}\)まで適合していて、なんとワンダフル。

• 

• 

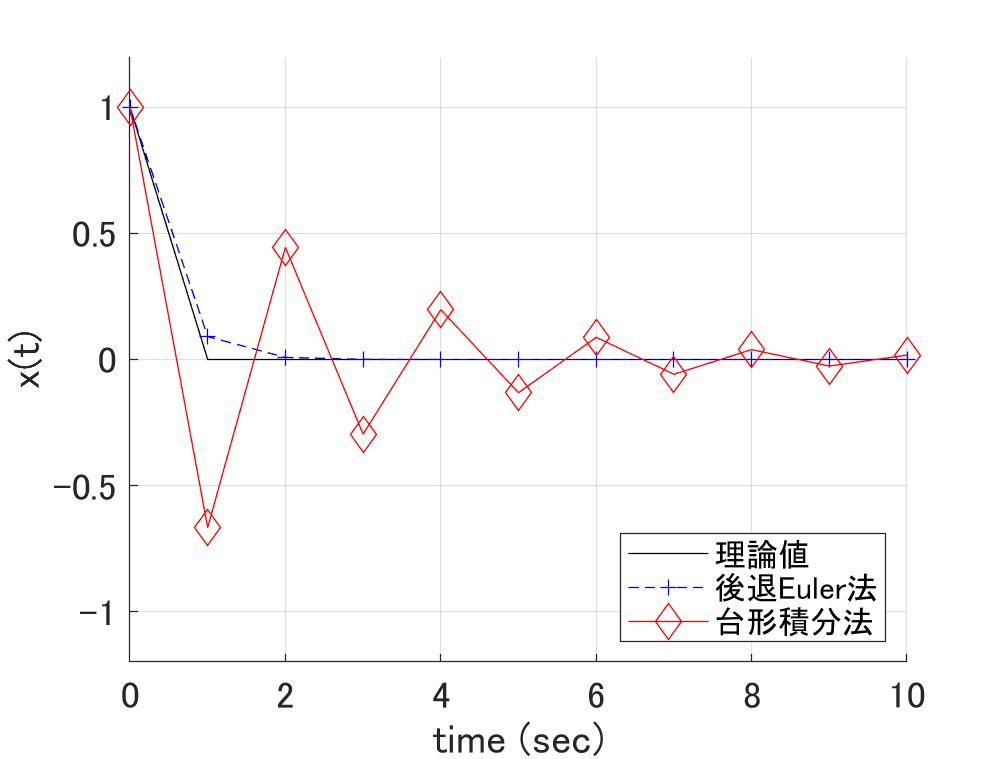
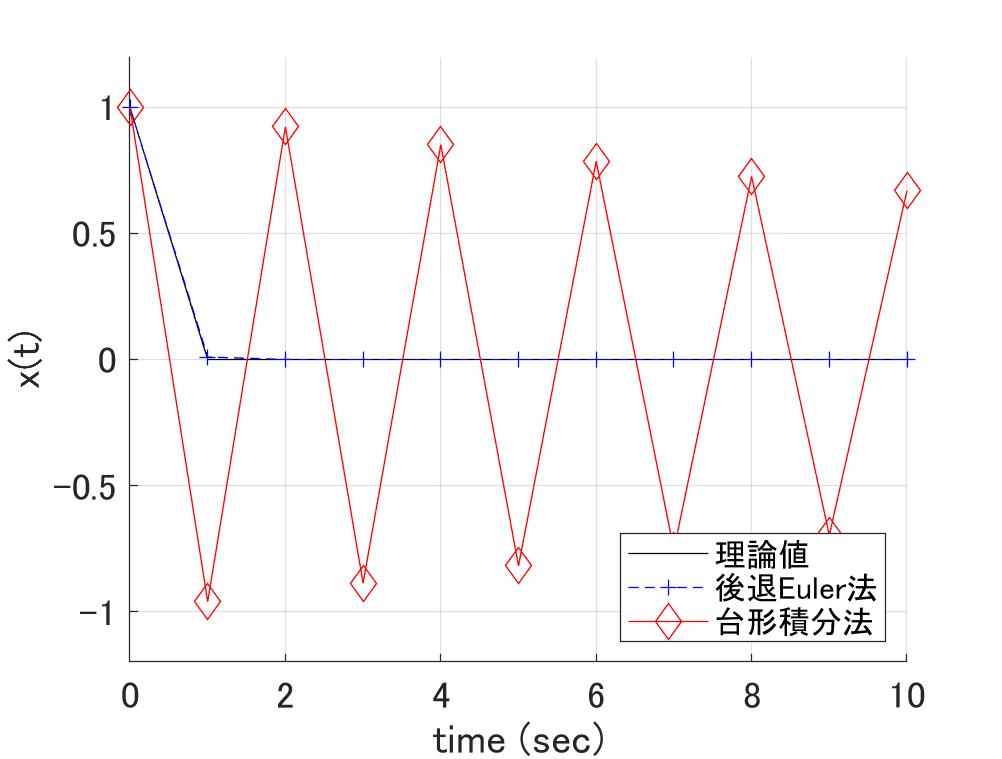
　図3a　\(h\lambda=\pm\pi i \)の場合　　　　図3b　\(h\lambda=-3\)（重根）の場合

さらに、式\eqref{eq:defMatExp_9}は順番に計算するだけなので、陽解放（Explicit-Method)です。反復計算は必要ありません。

をぉぉ、これこそがまちの制御屋が求めていた数値解法ではないですか？

この手法は、あまりに当たり前なのか、式\eqref{eq:diffExp_9}を計算するのがあまりに面倒なのか^[7] … Continue reading、線形に限定するのは数値計算屋の沽券にかかわるのか、教科書では見かけない手法です。
特に名称も決まっていないようです。
確かに式\eqref{eq:StateEq_9}をTaylor展開すれば得られるのでTaylor展開法と呼んでもよいのでしょうが、偏微分が出てこないTaylor展開法なんて。。。という気もします。

ですので、「N次指数関数法」と、呼ぶことにします。
あぁ、「N次指数関数法」に栄光あれ。

という、画期的な数値解法を掘り起こしたわけですが、
残念ながら、この手法は線形方程式限定です。

「線形方程式限定？　お客を選んだら、商売にならへんのや」
数値解法君の嘆く声が聞こえます^[8] … Continue reading。

やっぱ、任意関数でどうにかならんですかね？

前回、台形積分法に言いがかりをつけるにあたって、勢いで、
「台形積分法はL安定」ではない、とやったんですが、L安定とは、
「A安定でかつ、\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty}x_{i}=0\)」ですよね。\( Re(\lambda)\rightarrow-\infty\)なんて固有値を問題にしていいんでしょうか？虚軸方向は「Nyquist 周波数を超えたら意味はない」とブチかましておいて。

やはり、実数軸方向にも頃合いってもんがあるのでは？
ということで、前回の図4を再掲します。

• 

• 

図1a　\(h\lambda=-10\) 　　　　　　　　図1b　\(h\lambda=-100\)

計算しているのは、
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \qquad x(0)=1
\label{eq:Test}
\end{equation}
なので、ズバリ、
\begin{equation}
x(t) = e^{\lambda t}
\label{eq:AnSolution}
\end{equation}
が解析解ですが、例によって\(h=1\)で計算した場合、最初の1ステップ\((t=1)\)の値は
\(\lambda=-10\)の場合、\(e^{-10}=0.000045\)、
\(\lambda=-100\)の場合、\(e^{-100}=3.7201×10^{-44}\)
です。

ゼロの数を数えてくださいよ。計算初日（最初の1ステップ）で限りなくゼロです。過渡特性もなにもあったもんじゃない。
こんな固有値、計算する必要があるでしょうか？

という事で、実軸の固有値の限界を探ってみると、
\(h\lambda=-3\)の場合、\(e^{-3}=0.0498\)
\(h\lambda=-4\)の場合、\(e^{-4}=0.0183\)
\(h\lambda=-5\)の場合、\(e^{-5}=0.0067\)

\(h\lambda=-5\)までいけば、0.67%なので十分、2ステップ目からはさらにゼロに近づくことを考慮すれば、\(h\lambda=-4\)、\(h\lambda=-3\)でも大丈夫でしょう。

図2　\(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果

という事で、Stiffな方程式を計算するときに必要な安定領域は、虚数軸方向はNyquist 周波数ということで±3.14i、実数軸方向は-3の図3の領域で十分であり、必ずしもA安定である必要はない^[1] … Continue reading、というのが結論です。

図3　意味があると考える安定領域

「ですがね。計算しろよ！って渡された方程式が、都合の良い固有値を持ってる保証はないんですぜ、ダンナ」と数値解法君はおっしゃるでしょうね。

「しかしだ君。先ずは、安定領域内であれば、まともな精度で計算をやってあげるのが、君の誠というものではないかね、数値解法君？」

「安定であればどこでも、まともな計算精度」は少々厳しいので、まちの制御屋が意味があると断定した、実軸方向で\([-3,0]\)、虚軸方向で\([-\pi i,+\pi i]\)の範囲を安定領域に含み、この領域でまともな精度を持つ数値解法が欲しいところです。

4次のRunge-Kutta法は、残念ながら安定領域が足りません。陰解法に頼ろうにも、\(1<|h\lambda|\)の条件では、後退Euler法や台形積分法は適合次数が低く、Taylor級数の打ち切った項のタタリが怖すぎます^[2]虚軸方向で考察した、Taylor展開の収束の遅さは実軸でも同様。

これらを凌ぐ、安定領域が広く精度の高い手法はあるのでしょうか？
次回です。

参考文献
1: 「常微分方程式の数値解法　Ⅱ」 E. ハイラー G、ヴァンナー 三井　斌友　監訳　
2008年　シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド，
　　中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館

天下の台形積分法に言いがかりをつけるたぁいい度胸なんですが、つけます。
例によって、状態方程式
\begin{equation}
\frac{dX}{dt}=AX+Bf \\
\label{eq:StateEquation}
\end{equation}
\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
\:
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right]
\:
B= \left[
\begin{array}{c}
9.8 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
\(において、m=1　c=0\)で\(k=(2\pi)^2\)を\(h=1\)で計算すると、

図1　\(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果

となります。なんか台形積分法の計算結果が変ですね。いや、それ以上に理論値が変です。よく見るとゼロから微動だにしません。

「君ねぇ、1Hzの振動波形だろう。サンプル周波数\(=1Hz (h=1) \)じゃ、Nyquist周波数を超えてるんだよ」

という偉い人の声が聞こえそうです。
そうなんですよね。台形積分法は（後退Euler法も）極めて広い安定領域を持ちますが、Nyquist周波数を超えた振動を与える固有値の場合、例え安定に計算できても、それはデータとして表現できないんで意味ないんじゃないか？

というのが第一のイチャモンです。

数値計算の教科書や論文は、「Stiffな方程式を計算するには、左半平面全てを含むA安定でなければならない」、という空気を漂わせるのですが、

Nyquist 周波数を超えた固有値の安定性なんか、無視してもいいんじゃないでしょうか？

「わかった、その件は不問にするから、とっとと立ち去り給え」　また偉い人の声が聞こえてきます。

しかし、これなんかどうでしょうか？　\(k=\pi^2\)でぴったりNyquist 周波数です。

図2　\(h=1\)で\(0.5Hz\)の波形を台形積分法で計算した結果

無い袖を振って、Nyquist周波数に入れたのに、つれないです。

そこで第２のイチャモンですが、台形積分法は\(h\)の2次の精度なのですが、2次では次数が足りてないんじゃないか？　です。

数値解法とTaylor展開で書きましたが、台形積分法の近似精度はTaylor展開の2次までです。
テスト方程式と呼ばれる
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \\
\label{eq:Test}
\end{equation}
の場合は、Taylor展開＝指数関数となり、Taylor級数を\(\infty\)までもっていけば厳密解となりますので（常微分方程式と状態方程式）、
\begin{equation}
　x_{i+1}= \left( 1+h\lambda+\frac{(h\lambda)^2}{2}+\frac{(h\lambda)^3}{3!} 　+…+\frac{(h\lambda)^\infty}{\infty !}\right)x_i
\label{eq:Exponential}
\end{equation}
という計算になります。
ですが、式\eqref{eq:Exponential}の級数をよく見ると\(1<|hλ|\)の場合、\(n\)乗すると、分子がどんどん大きくなって収束しないんじゃないかと心配になります。

ですが、分母が「！」で表される、発散させたら宇宙一の「階乗さま」ですから、収束することは間違いないです。

とは言え、\(1<|hλ|\)だと、収束するのに、かなりの次数が必要だということも事実です。
今は\( h\lambda=\pi i \)を問題にしていますが、めんどくせ~ので\(h\lambda=3\)とすると、台形積分法の場合、3次の項\(\frac{3^3}{3!}=\frac{27}{6} \)で打ち切ってますが、こんな大きな項を無かった事にしちゃっていいんでしょうか？
せめて１以下にならないと腰が落ち着かないなら、\(3^6=729\)に対し、\(6!＝720\)ですので\(h\)の7次、あるいはそれ以上まで項を積まないといけません。

さらにもう一つイチャモン。と言うより、おそらくこの特性は専門家の間では周知であり、”台形積分法イマイチだね～”という特性かと思います。

式\eqref{eq:Test}で\(h\lambda=-1\)として台形積分法で計算すると、こうなります。

図3　式\(\eqref{eq:Test}\)での計算結果（\(h\lambda=-1\)）

この条件なら、台形積分法は後退Euler法など寄せ付けませんが、

• 

• 

図4a　\(h\lambda=-10\) 　　　　　　　　図4b　\(h\lambda=-100\)

図4a、図4bのように\(h\lambda\)の実数部の絶対値を大きくすると、計算が振動的になる。
なんじゃらほいということで、式\eqref{eq:Test}の台形積分法の計算式を確認すると、
\begin{eqnarray}
　 x_{i+1}&=&x_i+\frac{h}{2} (\lambda x_i + \lambda x_{i+1} \\
　(2 – h\lambda) x_{i+1}&=& (2 + h\lambda )x_i \\
x_{i+1} &=& \frac{(2 + h\lambda)}{ (2 – h\lambda)} x_i
\label{eq:Trapezoidal}
\end{eqnarray}
ここで、\(Re(\lambda) \rightarrow -\infty \)だとしましょう。式\eqref{eq:Trapezoidal}は
\begin{equation}
　x_{i+1} =- x_i
\end{equation}
になりますから、プラスとマイナスをいったりきたりです。

このようにテスト方程式で、A安定でありかつ\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty} x_{i}=0 \)となる特性を、L安定と呼んでいるようで^[1]Wikipediaは英語版のみです。日本語の文献では見かけませんが、参考文献1にはしっかり記載されています、「台形積分法はL-Stableでないから。。。」^[2]ちなみに後退Euler法はL-Stableと知ったかぶるのがナウいようです（この場合はL-Stalbeね）

というわけで、台形積分法に対する言いがかりをまとめます。

１：台形積積分法はA安定（左半平面全体を安定領域とする）だが、Nyquist周波数を超えた領域は計算できても結果を正しく表現できないので、それほどのありがたみは無い。

２：\(1<|hλ|\)のような固有値は、2次や3次の計算アルゴリズムでは、かなり大きな誤差が生じるため、実用的ではない。

３：L安定でないから、実数部の絶対値の大きな固有値は安定領域であっても計算結果が振動的になってよろしくない。

言いたいことは、「台形積分法は、確かに広大な安定領域を持ってますが、意味のある固有値の範囲はごく一部だけ。一方2次という適合次数では、その意味のある固有値の多くで計算精度が足りない」ということです。

しかしながら、であっても、計算が発散してしまっては話にならないので、かつ非線形関数の場合、固有値を計算するのが面倒（かつL安定に関しては日本人は気が付いてない）なので、A安定である台形積分法は有用^[3] … Continue reading、というところですが、おそらく一番の魅力は、時間軸対象アルゴリズムなので、系のエネルギーが（計算誤差を除き）勝手に増減しないため、持続振動波形を長時間計算可能ということなんでしょう。
確かにこの点は買えます。

参考文献
1: 「常微分方程式の数値解法　Ⅱ」 E. ハイラー G、ヴァンナー 三井　斌友　監訳　
2008年　シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド，
　　中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館