２：数値解法の安定性

常微分方程式で解析解が得られるのは、運が良いからだ、というのが定説ですので、一般的には数値計算に頼ることになりますが、そう言うと、「計算精度はどうなの？」という話になります。

ですが、制御屋は精度より、安定性を気にします。

\begin{equation}
\frac{dx(t)}{dt} = \lambda x(t)
\label{eq:scalar}
\end{equation}
という常微分方程式の解は、以前書いた「１：常微分方程式と状態方程式」より
\begin{equation}
x(t) = e^{\lambda t} x(0)
\end{equation}
ですが、ここで複素数である\(\lambda\)の実数部が正であると、\(e^{\lambda t}\)は、\(t\)が増えるにつれ、正に指数関数的に増加するので、無限大まで突っ走るしかありませんが、逆に実数部が負であれば、漸近的に零に収束し、何らかの解が得られることになります

一方、数値計算を行う場合ですが、例えば式(\ref{eq:scalar})の微分演算を、微小な値である\(h\)の間の差であると、かなり大雑把に考えれば、
\begin{equation}
\frac{dx}{dt} \simeq \frac{x_{i+1}-x_i}{h} =\lambda x_i
\end{equation}
\begin{equation}
x_i=x(t_i) \quad x_{i+1}=x(h+t_i) \nonumber
\end{equation}
となり、
\begin{equation}
　　　x_{i+1}=x_i+h\lambda x_i
　　　\label{eq:F_Euler}
\end{equation}
ですので、\(x_i\)から\(x_{i+1}\)を順次計算することができます。これが前進Euler法と呼ばれる数値計算手法です。

ここで式\eqref{eq:F_Euler}は
\begin{equation}
x_{i+1}=(1+h\lambda) x_i
\end{equation}
ですので、\((1+h\lambda)\)の絶対値が\(１\)より大きければ、\(x_i\)に対して\(x_{i+1}\)は常に大きくなるので、やはり無限大まで突っ走ってしまいます。

つまり、前進Euler法は\(h\lambda\)が

\begin{equation}
|1+h\lambda|<1
\label{eq:FEStableCond}
\end{equation}
を満たさない限り、計算が発散するのです。

式(\ref{eq:FEStableCond})の\(λ\)は複素数を認めますので、式(\ref{eq:FEStableCond})を図示すると、図1の複素平面内の単位円の内側が安定領域という事になります。

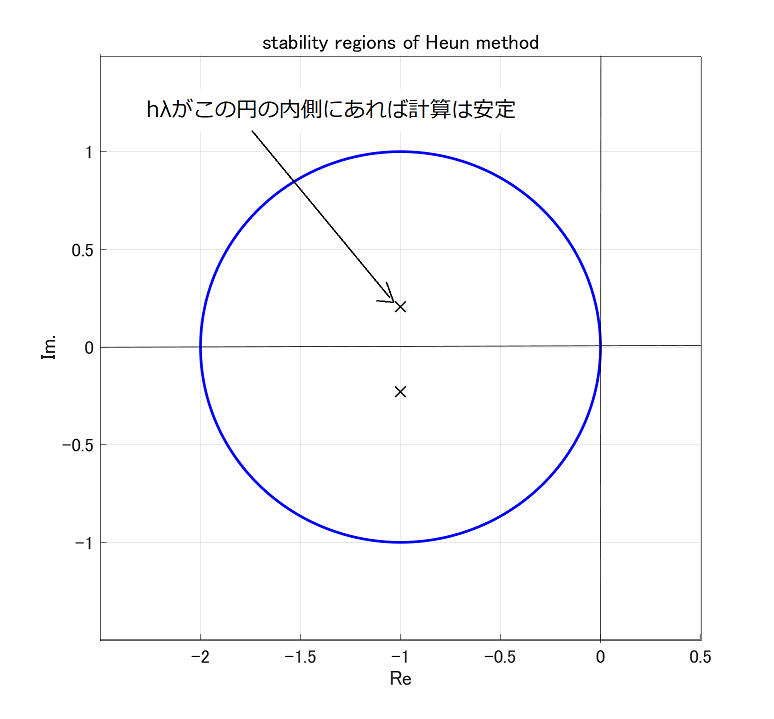
図1　前進Euler法の安定領域

元々の微分方程式である式\eqref{eq:scalar}では、\(\lambda\) の実数部が負であれば安定でしたが、前進Euler法の場合は、虚数部も含めて所定の範囲内でなければならない、と条件が厳しくなります。

しかしながら、\(h\)を掛けているので、\(\lambda\) が大くてはみ出しそう、という場合は\(h\)を小さくして対抗することができます。
その結果、「計算が発散する？　ならステップサイズ(\(=h\))を小さくしろ！」という声があちこちから聞こえることになります。

さて、話は変わりますが、「改良Euler法(Improved Euler Method)」というものがあります^[1]ここでいう改良Euler法は陽的台形法の事ですが、中点を用いる修正Euler法(Modified Euler … Continue reading。

前進Euler法ではあまりに大雑把なので、”改良”したわけですが、
\begin{equation}
x_{i+1}=x_{i}+{\frac {1}{2}}h(f(t_{i},x_{i}) + f(t_{i+1},x_{i}+hf(t_{i},x_{i})) )
\label{eq:HeunMethod}
\end{equation}
という計算式で、計算誤差は\(h\)の2乗に応じて減少する事になっており、常微分方程式を構成する関数を２回計算するだけで、誤差が大幅に小さくなるオトクな計算法ですが、これを式\eqref{eq:scalar}に適用すると、
\begin{eqnarray}
x_{i+1}&=&x_{i}+{\frac {1}{2}} h (\lambda x_{i} + \lambda (x_i + h \lambda x_i) )\nonumber \\
&=&x_{i}+ h \lambda x_{i} + {\frac {1}{2}} (h \lambda)^2 x_i
\end{eqnarray}
ですので、
\begin{equation}
\left|1+h\lambda+\frac{(h\lambda)^2}{2} \right|<1
\label{eq:HeunStableCond}
\end{equation}
が安定条件となり、図示すると、

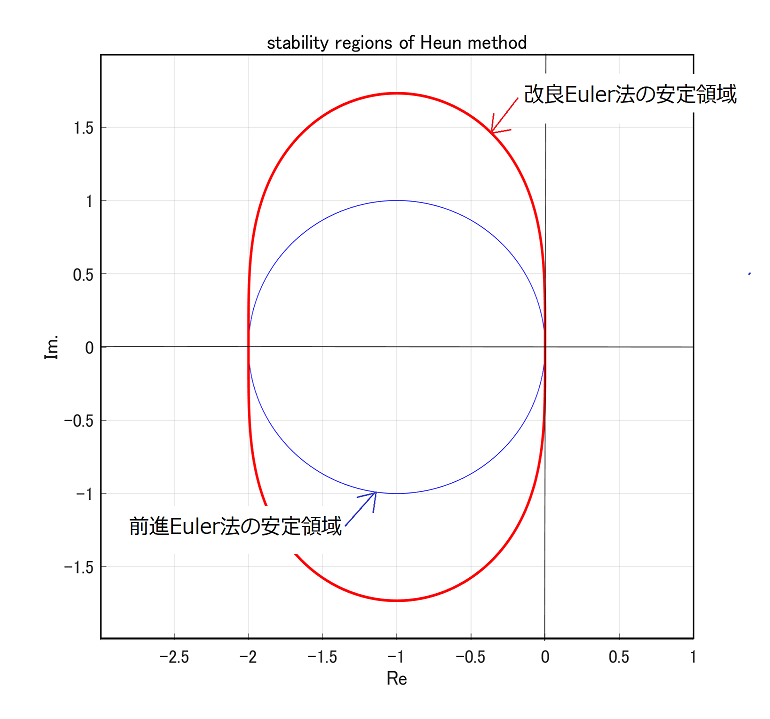
図2　改良Euler（Heun)法の安定領域

前進Eulerより安定領域が広がりました。数値計算は、計算手順を変えれば精度だけでなく、安定性も変わるのです。

こうなれば、あとは\(h\)で頑張れば、どんな\(\lambda\)が来ても大丈夫・・・ とはなりません。
この図ではわかりにくいですが、\(\lambda\)が虚軸上にあるとhをどんなに小さくしても、厳密には安定領域には入らないのです。
\(\lambda\)が虚軸上にあるというのは、減衰のない振動が持続するケースですが、その場合は、改良Euler法はいかがなものか？　となります^[2]をそれなりに小さくすれば、安定領域にかなり近いところになり、徐々に発散するため、実用的にはOK、という場合もあります。

ここで、真打の登場です。

常微分方程式の計算といえば、4次のRunge-Kutta法に止めを刺す、と長らく言われておりました。
\begin{eqnarray}
x_{i+1}&=&x_{i}+{\frac {h}{6}}(k_1+2k_2 + 2k_3+k_4)\nonumber \\
k_1&=&f(t_{i}\; , \; x_{i})\nonumber \\
k_2&=&f(t_{i}+\frac{h}{2}\; , \; x_{i}+\frac{h}{2}k_1)\nonumber \\
k_3&=&f(t_{i}+\frac{h}{2}\; , \; x_{i}+\frac{h}{2}k_2)\nonumber \\
k_4&=&f(t_{i}+h\; , \; x_{i}+hk_3)
\end{eqnarray}

4次のRunge-Kutta法は、その名のとおり\(h\)の4次の精度を持ち^[3]Taylor展開で与えられる厳密解に対し、\(h\)の4次の項まで一致する、関数を4回計算すれば4次の精度が得られる、オトクでお値打ちな計算法で、さらに安定条件は
\begin{equation}
\left|1+h\lambda+\frac{(h\lambda)^2}{2} + \frac{(h\lambda)^3}{2\cdot3} + \frac{(h\lambda)^4}{4!}　\right|<1
\label{eq:ClassicRKStableCond}
\end{equation}
です。

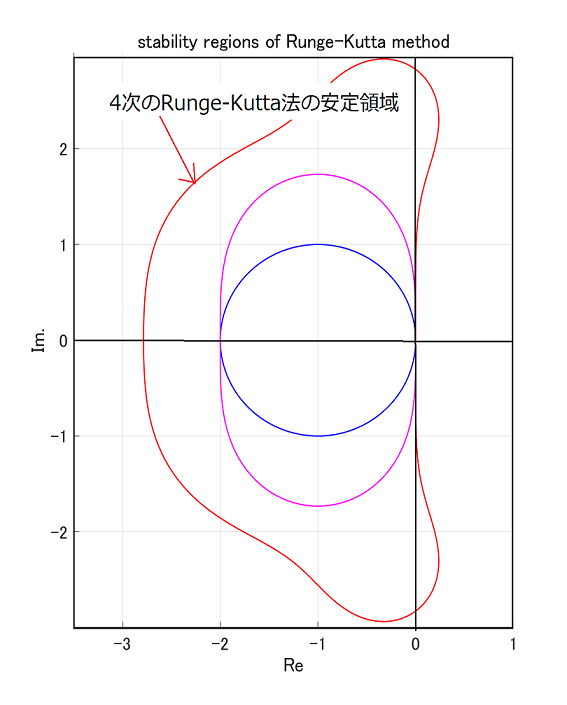
4次のRunge-Kutta法の安定領域

おおっ！かなり広い安定領域。しかも虚軸も含まれているではないですか！　これで、もう安心、あとは何があっても\(h\)で頑張る、。。。という時代もあったのですが、現在では、いやこのBlogではそれは許しません。

なぜなら、Stiffに弱いから

ということで、次回に続きます。