天下の台形積分法に言いがかりをつけるたぁいい度胸なんですが、つけます。
例によって、状態方程式
\begin{equation}
\frac{dX}{dt}=AX+Bf \\
\label{eq:StateEquation}
\end{equation}
\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
\:
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right]
\:
B= \left[
\begin{array}{c}
9.8 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
\(において、m=1 c=0\)で\(k=(2\pi)^2\)を\(h=1\)で計算すると、
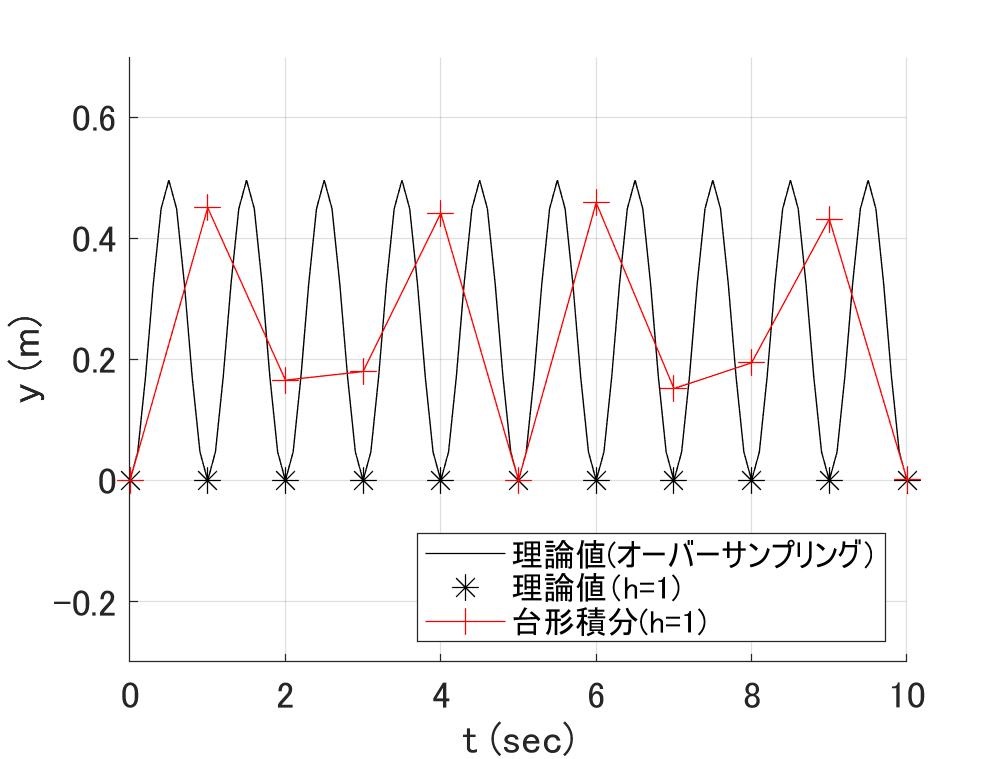
図1 \(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果
となります。なんか台形積分法の計算結果が変ですね。いや、それ以上に理論値が変です。よく見るとゼロから微動だにしません。
「君ねぇ、1Hzの振動波形だろう。サンプル周波数\(=1Hz (h=1) \)じゃ、Nyquist周波数を超えてるんだよ」
という偉い人の声が聞こえそうです。
そうなんですよね。台形積分法は(後退Euler法も)極めて広い安定領域を持ちますが、Nyquist周波数を超えた振動を与える固有値の場合、例え安定に計算できても、それはデータとして表現できないんで意味ないんじゃないか?
というのが第一のイチャモンです。
数値計算の教科書や論文は、「Stiffな方程式を計算するには、左半平面全てを含むA安定でなければならない」、という空気を漂わせるのですが、
Nyquist 周波数を超えた固有値の安定性なんか、無視してもいいんじゃないでしょうか?
「わかった、その件は不問にするから、とっとと立ち去り給え」 また偉い人の声が聞こえてきます。
しかし、これなんかどうでしょうか? \(k=\pi^2\)でぴったりNyquist 周波数です。
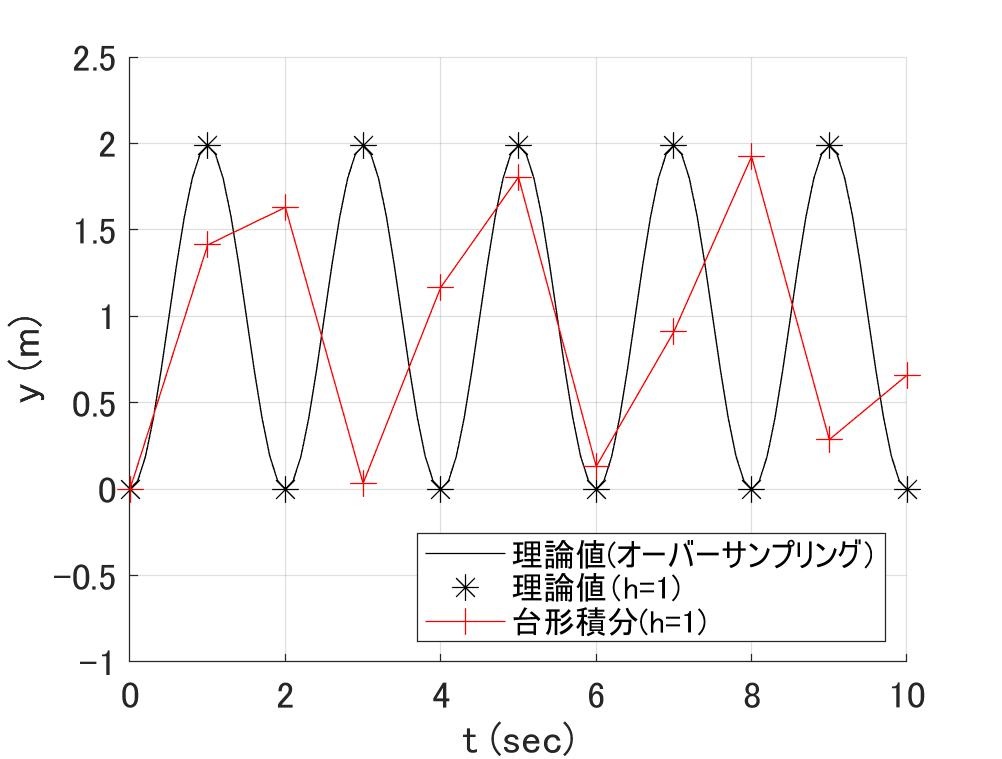
図2 \(h=1\)で\(0.5Hz\)の波形を台形積分法で計算した結果
無い袖を振って、Nyquist周波数に入れたのに、つれないです。
そこで第2のイチャモンですが、台形積分法は\(h\)の2次の精度なのですが、2次では次数が足りてないんじゃないか? です。
数値解法とTaylor展開で書きましたが、台形積分法の近似精度はTaylor展開の2次までです。
テスト方程式と呼ばれる
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \\
\label{eq:Test}
\end{equation}
の場合は、Taylor展開=指数関数となり、Taylor級数を\(\infty\)までもっていけば厳密解となりますので(常微分方程式と状態方程式)、
\begin{equation}
x_{i+1}= \left( 1+h\lambda+\frac{(h\lambda)^2}{2}+\frac{(h\lambda)^3}{3!} +…+\frac{(h\lambda)^\infty}{\infty !}\right)x_i
\label{eq:Exponential}
\end{equation}
という計算になります。
ですが、式\eqref{eq:Exponential}の級数をよく見ると\(1<|hλ|\)の場合、\(n\)乗すると、分子がどんどん大きくなって収束しないんじゃないかと心配になります。
ですが、分母が「!」で表される、発散させたら宇宙一の「階乗さま」ですから、収束することは間違いないです。
とは言え、\(1<|hλ|\)だと、収束するのに、かなりの次数が必要だということも事実です。
今は\( h\lambda=\pi i \)を問題にしていますが、めんどくせ~ので\(h\lambda=3\)とすると、台形積分法の場合、3次の項\(\frac{3^3}{3!}=\frac{27}{6} \)で打ち切ってますが、こんな大きな項を無かった事にしちゃっていいんでしょうか?
せめて1以下にならないと腰が落ち着かないなら、\(3^6=729\)に対し、\(6!=720\)ですので\(h\)の7次、あるいはそれ以上まで項を積まないといけません。
さらにもう一つイチャモン。と言うより、おそらくこの特性は専門家の間では周知であり、”台形積分法イマイチだね~”という特性かと思います。
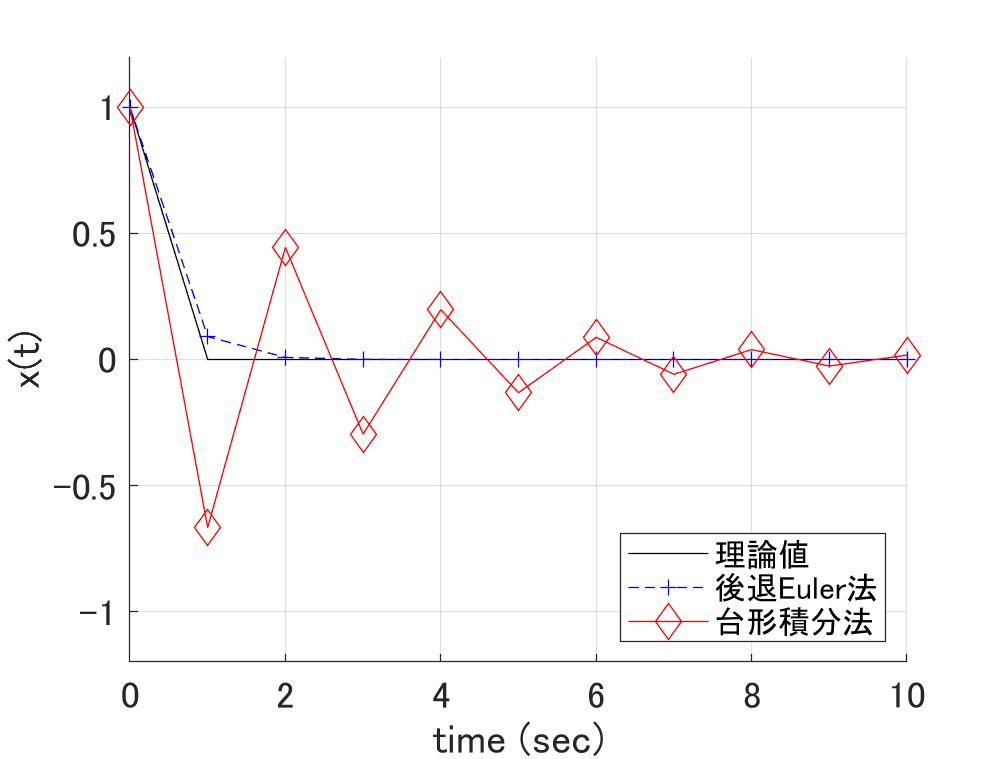
式\eqref{eq:Test}で\(h\lambda=-1\)として台形積分法で計算すると、こうなります。
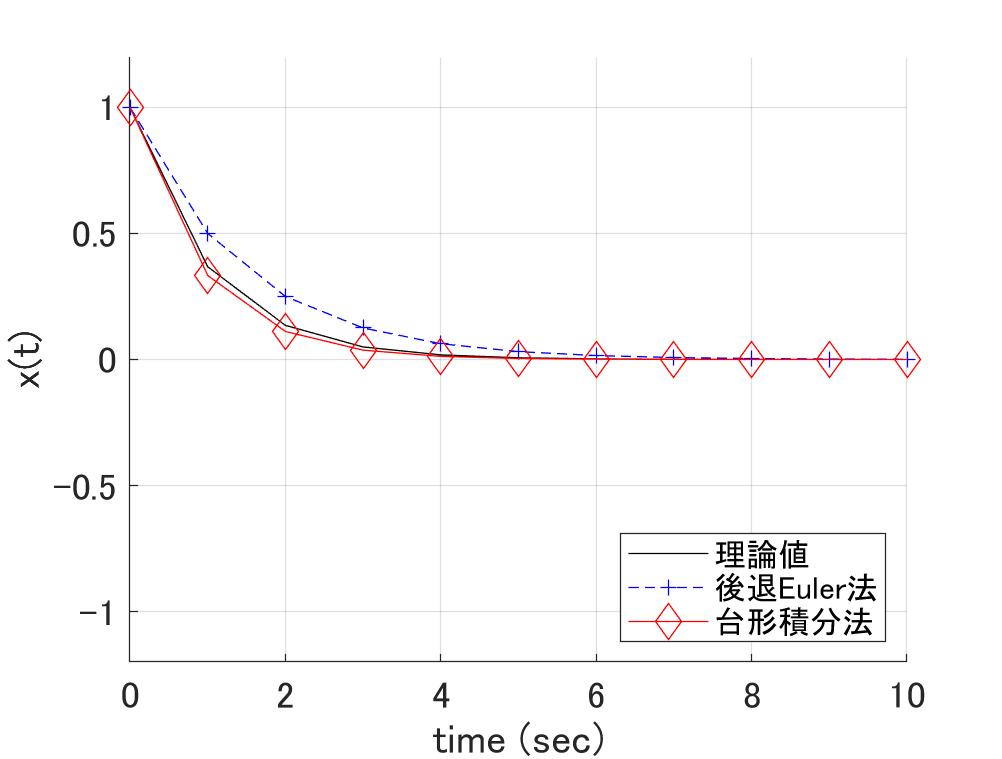
図3 式\(\eqref{eq:Test}\)での計算結果(\(h\lambda=-1\))
この条件なら、台形積分法は後退Euler法など寄せ付けませんが、
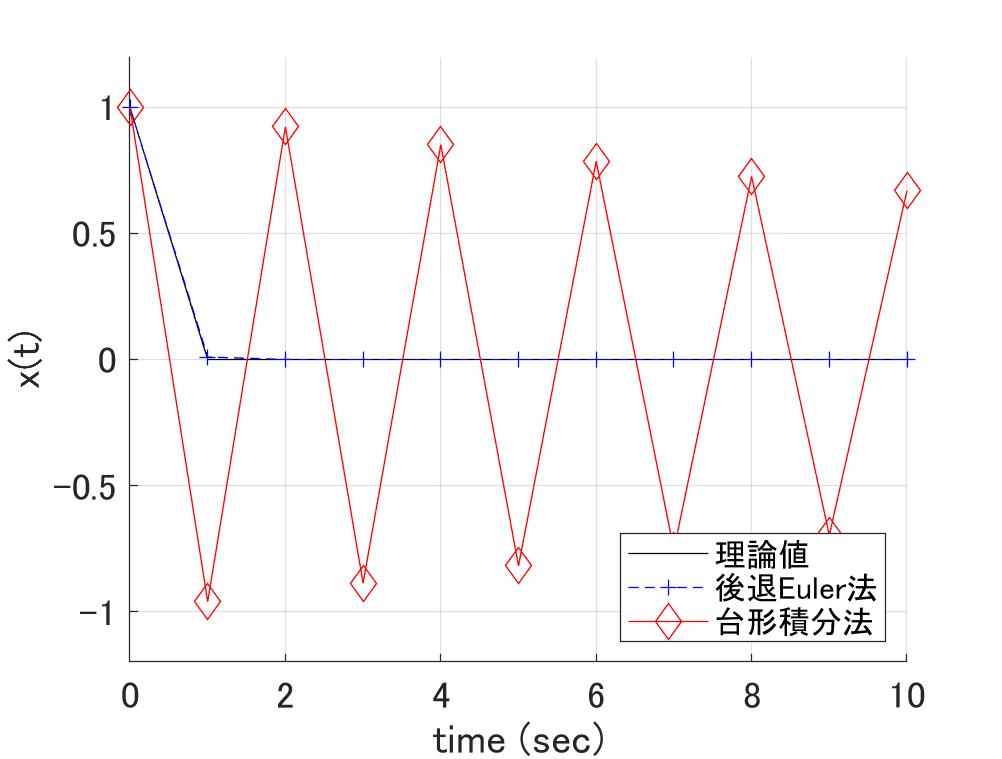
図4a \(h\lambda=-10\) 図4b \(h\lambda=-100\)
図4a、図4bのように\(h\lambda\)の実数部の絶対値を大きくすると、計算が振動的になる。
なんじゃらほいということで、式\eqref{eq:Test}の台形積分法の計算式を確認すると、
\begin{eqnarray}
x_{i+1}&=&x_i+\frac{h}{2} (\lambda x_i + \lambda x_{i+1} \\
(2 – h\lambda) x_{i+1}&=& (2 + h\lambda )x_i \\
x_{i+1} &=& \frac{(2 + h\lambda)}{ (2 – h\lambda)} x_i
\label{eq:Trapezoidal}
\end{eqnarray}
ここで、\(Re(\lambda) \rightarrow -\infty \)だとしましょう。式\eqref{eq:Trapezoidal}は
\begin{equation}
x_{i+1} =- x_i
\end{equation}
になりますから、プラスとマイナスをいったりきたりです。
このようにテスト方程式で、A安定でありかつ\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty} x_{i}=0 \)となる特性を、L安定と呼んでいるようで[1]Wikipediaは英語版のみです。日本語の文献では見かけませんが、参考文献1にはしっかり記載されています、「台形積分法はL-Stableでないから。。。」[2]ちなみに後退Euler法はL-Stableと知ったかぶるのがナウいようです(この場合はL-Stalbeね)
というわけで、台形積分法に対する言いがかりをまとめます。
1:台形積積分法はA安定(左半平面全体を安定領域とする)だが、Nyquist周波数を超えた領域は計算できても結果を正しく表現できないので、それほどのありがたみは無い。
2:\(1<|hλ|\)のような固有値は、2次や3次の計算アルゴリズムでは、かなり大きな誤差が生じるため、実用的ではない。
3:L安定でないから、実数部の絶対値の大きな固有値は安定領域であっても計算結果が振動的になってよろしくない。
言いたいことは、「台形積分法は、確かに広大な安定領域を持ってますが、意味のある固有値の範囲はごく一部だけ。一方2次という適合次数では、その意味のある固有値の多くで計算精度が足りない」ということです。
しかしながら、であっても、計算が発散してしまっては話にならないので、かつ非線形関数の場合、固有値を計算するのが面倒(かつL安定に関しては日本人は気が付いてない)なので、A安定である台形積分法は有用[3] … Continue reading、というところですが、おそらく一番の魅力は、時間軸対象アルゴリズムなので、系のエネルギーが(計算誤差を除き)勝手に増減しないため、持続振動波形を長時間計算可能ということなんでしょう。
確かにこの点は買えます。
参考文献
1: 「常微分方程式の数値解法 Ⅱ」 E. ハイラー G、ヴァンナー 三井 斌友 監訳
2008年 シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー,L.R.ペツォルド,
中村 眞理雄 監訳 嘉村友作・三ツ間 均 共訳 2006年 培風館