投稿者: まちの制御屋

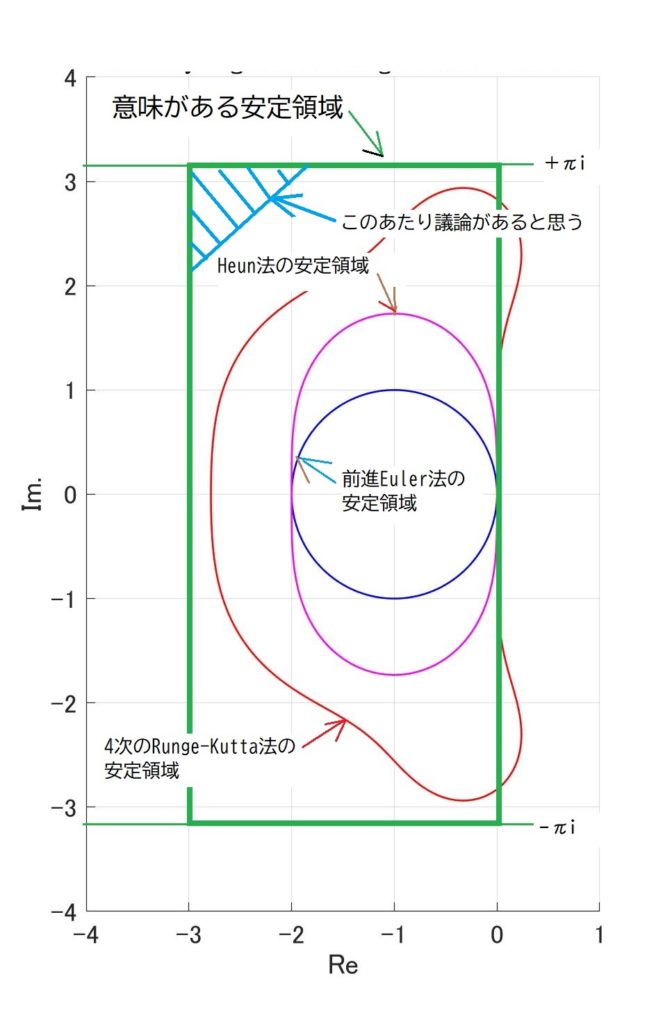
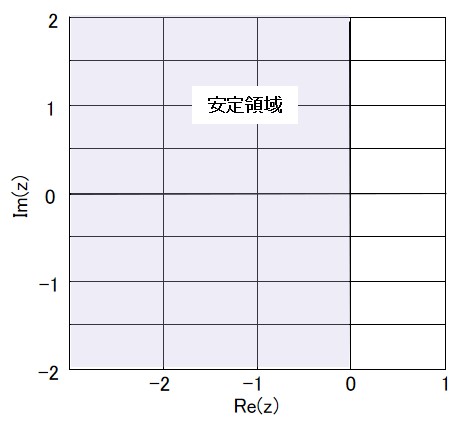
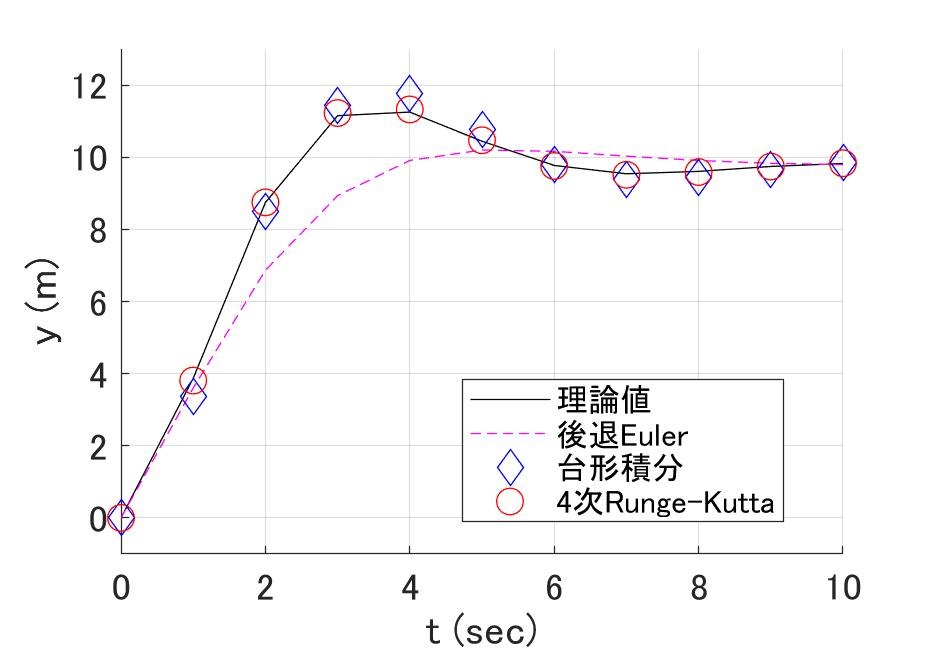
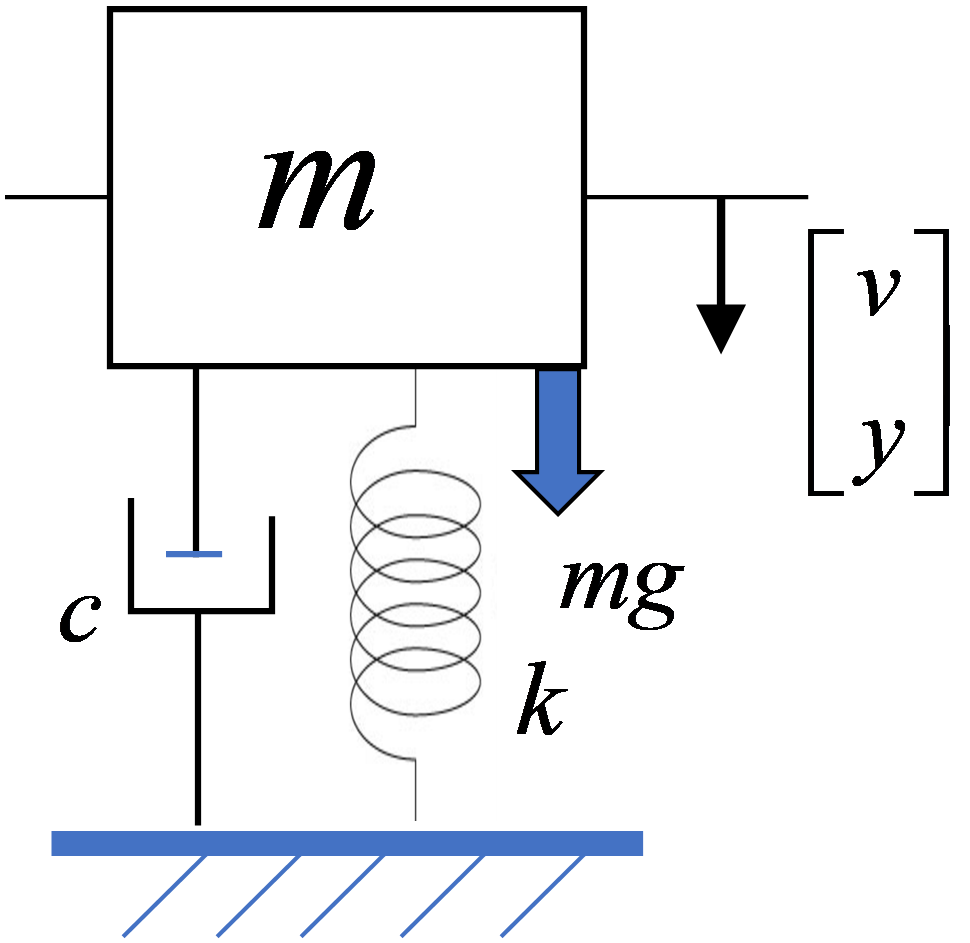
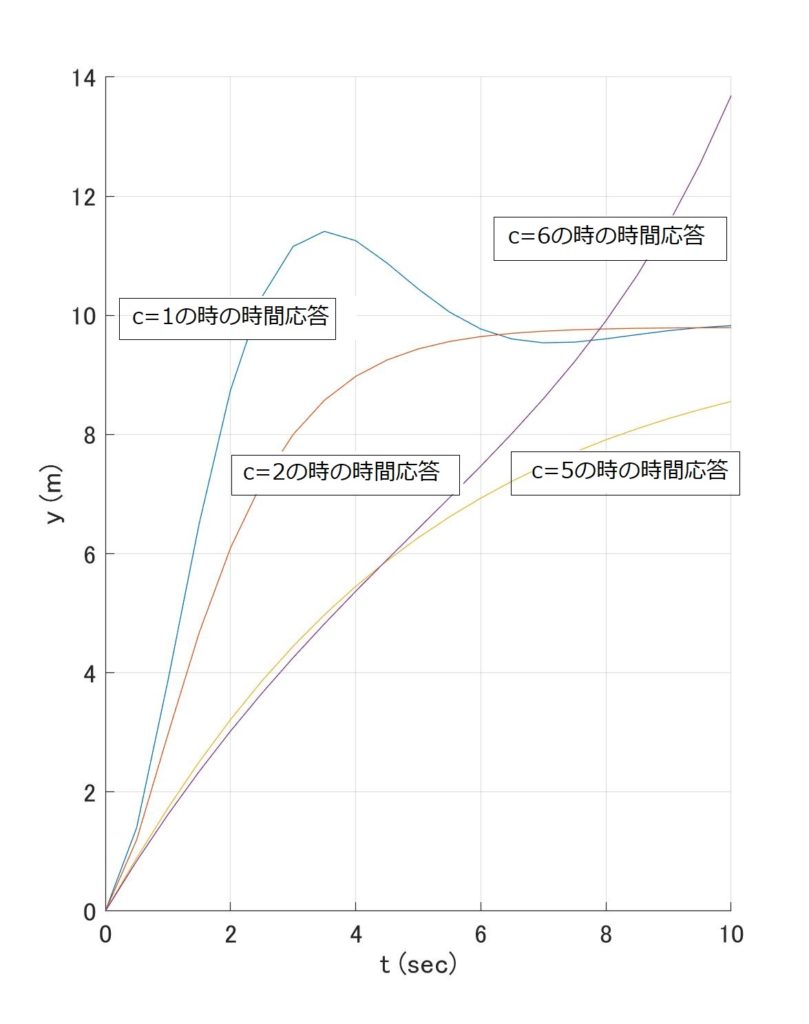
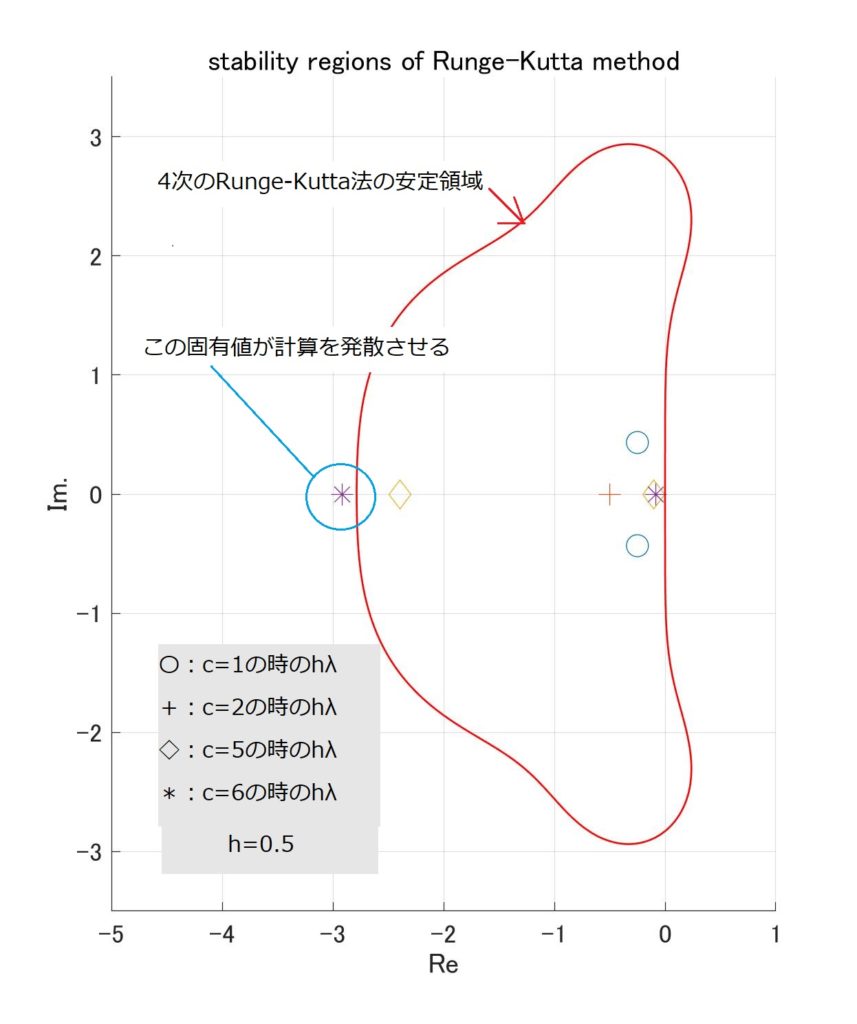
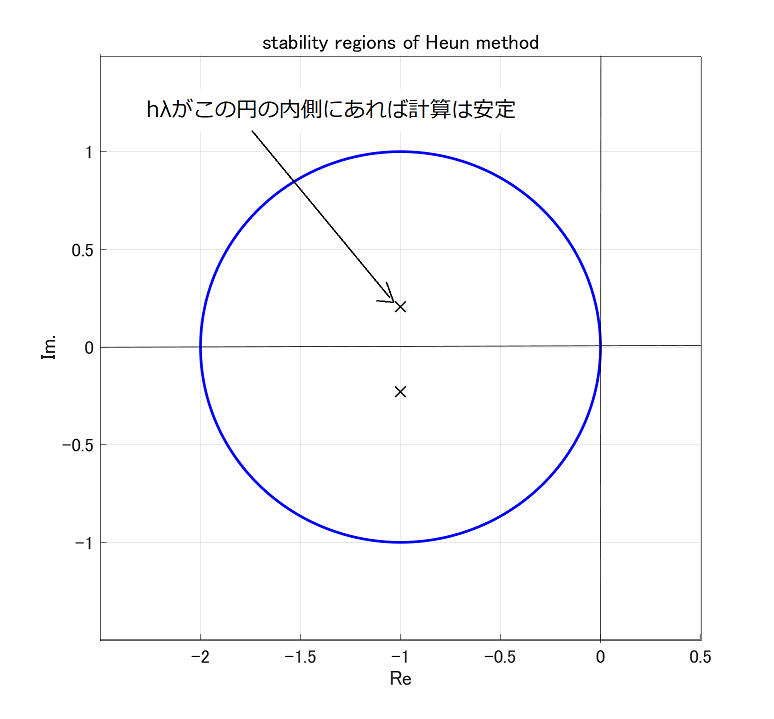
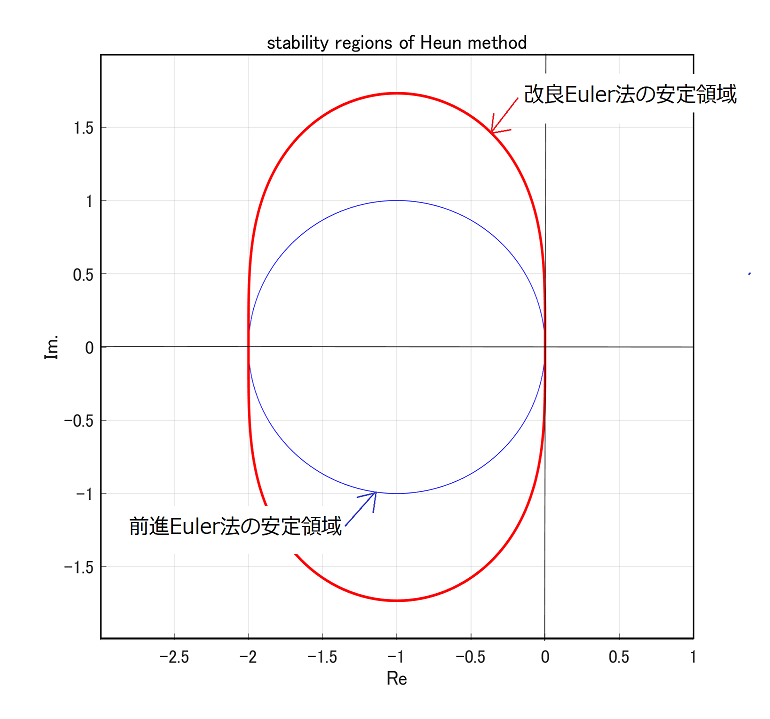
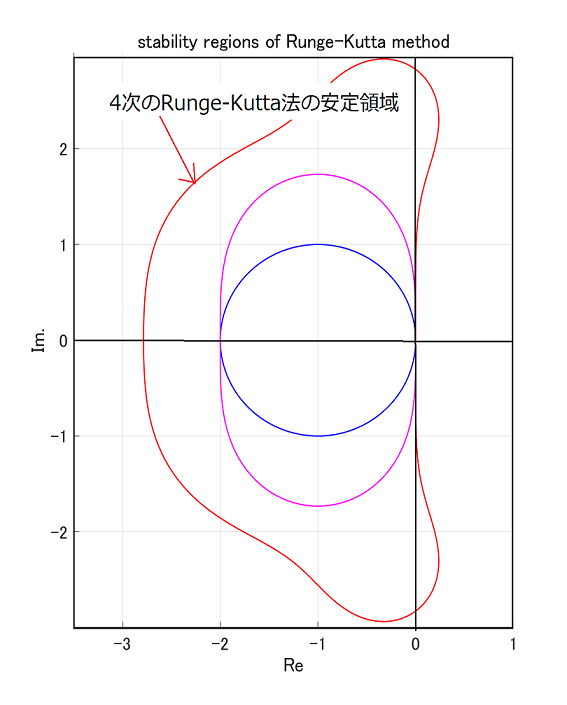
前回、必要な安定領域は実軸方向で\([-3,0]\)、虚軸方向で\([-\pi i,+\pi i]\)の範囲と勝手に決めつけたわけですが、この領域で安定でまともな計算精度がある数値解法はあるのでしょうか？
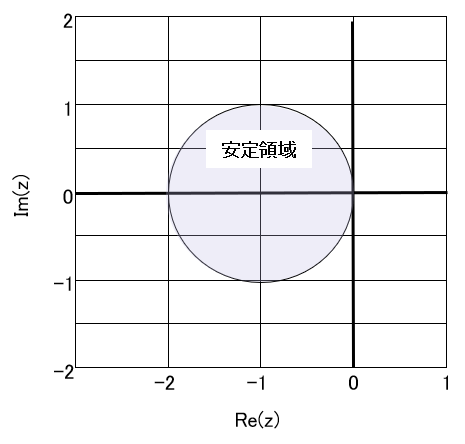
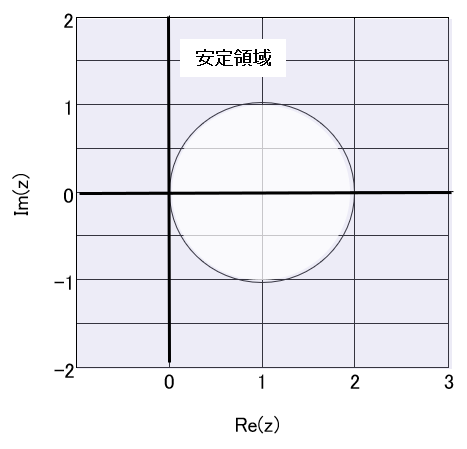
いずれじっくりやりたいと思いますが、こういう場合の定番の後退微分法（BDF）やAdams-Moulton法が候補に入らなことは事は図1^[1]いずれじっくりやりますので、図が甘いのはご容赦くださいで示しておきます。
後退微分法（Gear法とも言う）は3段^[2]Wikipediaの訳に従い”段”としましたが、英語ではStepです。Runge-Kutta法のときは、Stageを段と訳しているので、非常に紛らわしいの場合は（緑の線）と虚軸がわずかに安定領域から外れ、4段になるとオイシイ領域が不安定になり、6段を超えると不安定という、実はけっこう痛い奴です^[3]Stiff-Solverの代表格である後退微分法は3次以上はA安定じゃない、というのが衝撃の事実。

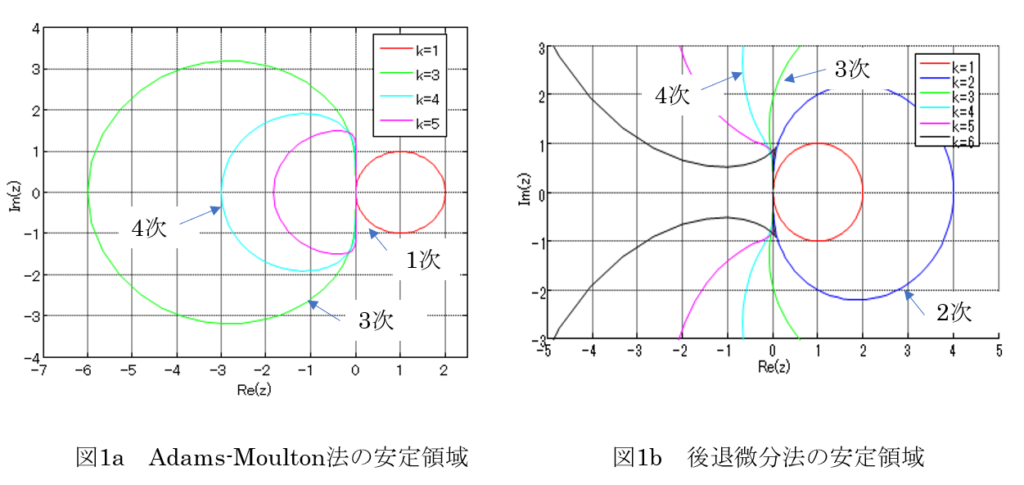
おや、台形積分も、後退Eulerも、Adams-Moultonも、Gearも、全部だめなら、候補は残るのか？

それがあります。線形式に限定すれば、ありえます。

最初の「常微分方程式と状態方程式」で書きましたが、線形の常微分方程式である状態方程式
\begin{equation}
\frac{dX(t)}{dt}=AX(t)+BU(t)
\label {eq:StateEq_9}
\end{equation}
の場合、\(X_i=X(t_0)、　X_{i+1}=X(h+t_0)\)とすれば、
\begin{equation}
X_{i+1}=e^{A h}X_i + (e^{A h} – I )A^{-1} BU_i
\label{eq:diffExp_9}
\end{equation}
となるので式\eqref{eq:diffExp_9}を計算すれば、\(X_iからX_{i+1}\)が即座に得られますよね、と。

ですが、行列指数関数\(e^{A}\)は、
\begin{equation}
e^{A}:=I+A+\frac{A^2}{2!}+…+\frac{A^N}{N!}= \sum_{k=0}^{N} \frac{A^k}{k!}
\label{eq:defMatExp_9}
\end{equation}
において\(N\rightarrow\infty\)なんですが、これはどうやって計算するのでしょうか？
式\eqref{eq:defMatExp_9}をそもまま頑張って計算する？　\(N=\infty\)まで？

たしかに、\(\infty\)まではできませんが、この手の式の高次項は収束するのがお約束なので適当なところまで頑張ればOK、のはずです。適当なところまで頑張ってみましょう。

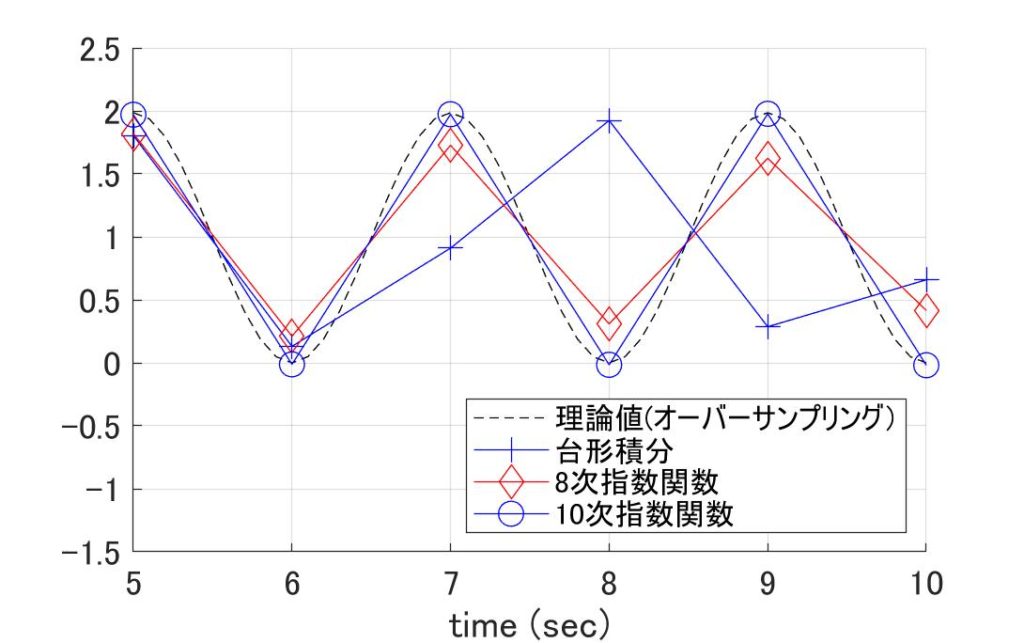
しかし、「台形積分法に言いがかりをつける」でも書きましたが、\(h\lambda=3\)の場合\(( 3^k/k! )\)が１より小さくなるのは\(k=7\)の時です。従って、少なくとも\(N=7\)を超えないとマズそうなので、イロを付けて\(N=10\)まで頑張ってみたのが図2です。

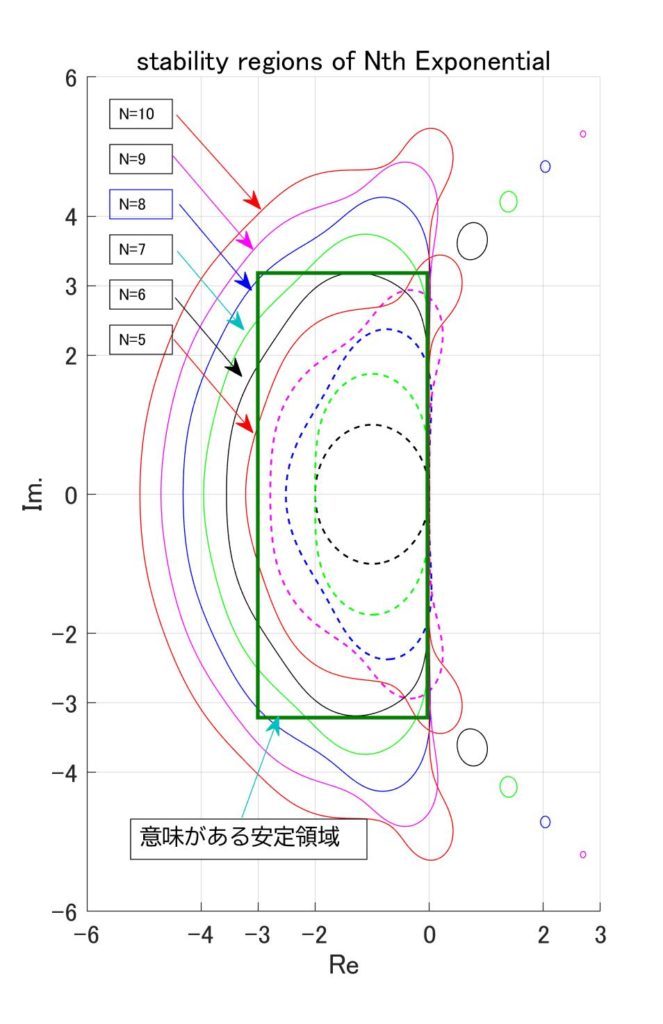
図2　N次で打ち切った指数関数の安定領域

式\eqref{eq:defMatExp_9}の行列指数関数を\(N\)次で打ち切ったものを使用して、式\eqref{eq:diffExp_9}を計算した場合の安定領域は、実はRunge-Kutta法と同じ^[4]「Taylor展開とRunge-Kutta法」の時にやりましたなので、4次まではよく見かけると思いますが、5次から先は初めて見たのではないでしょうか？
まちの制御屋もこの図2が出てくる論文^[5]”On the absolute stability regions corresponding to partial sums of the exponential function” D.Ketchenson et al. IMA Journal of Numerical Analysis, Volume 35, Issue 3, July 2015, Pages … Continue readingを見つけたときは、胸が張り裂けそうでした。

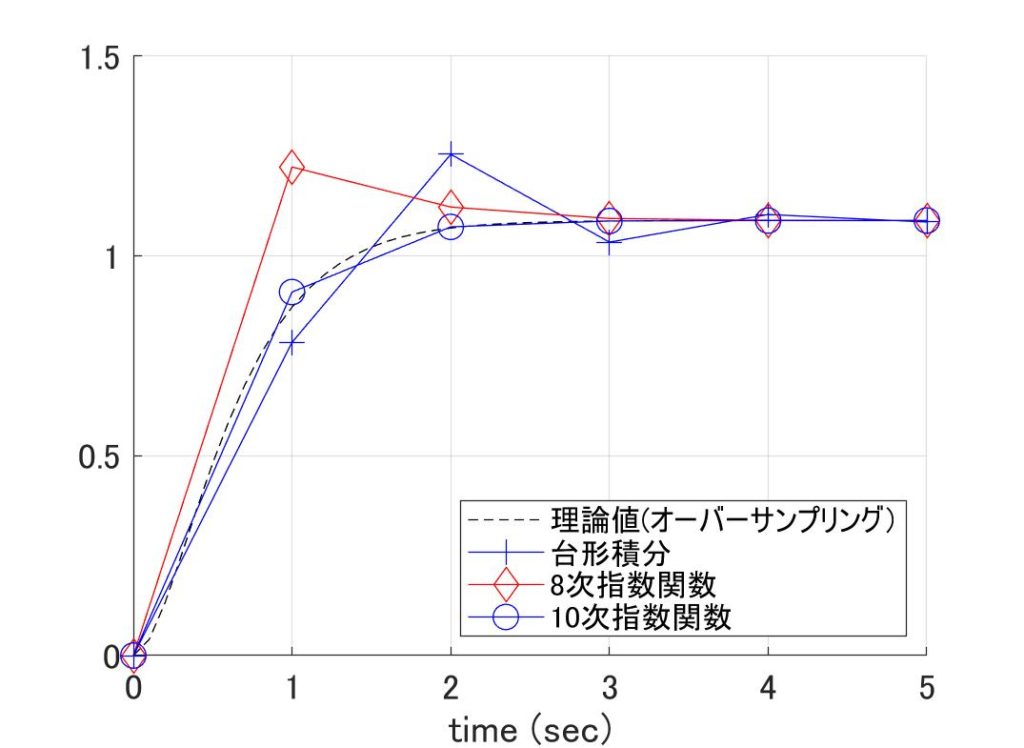
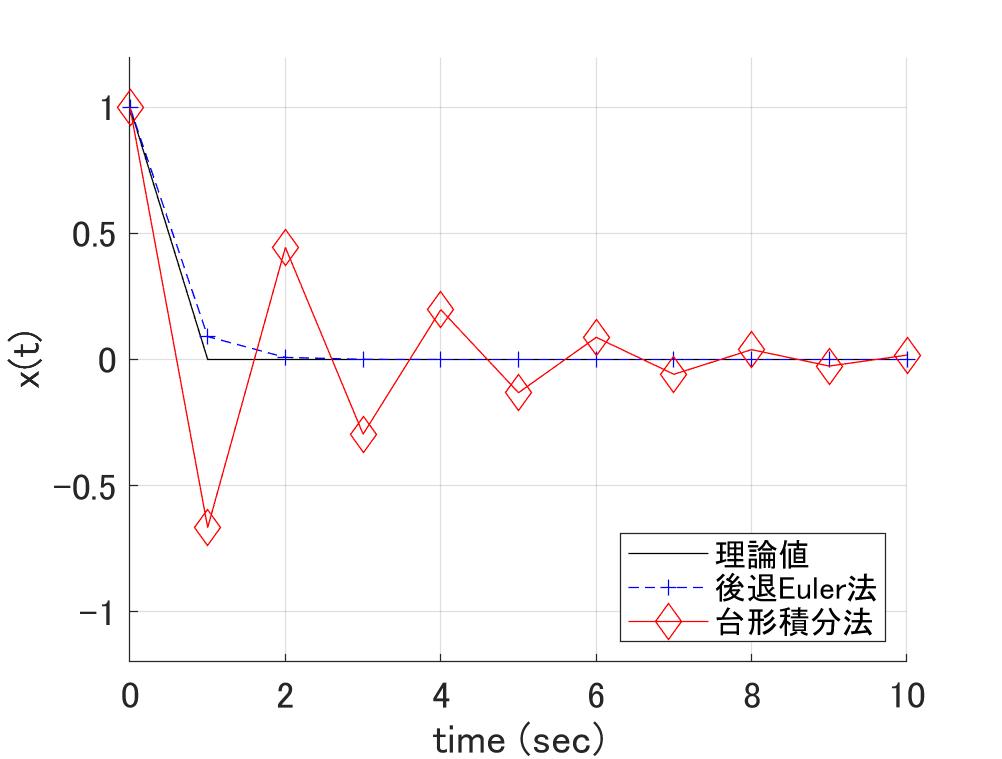
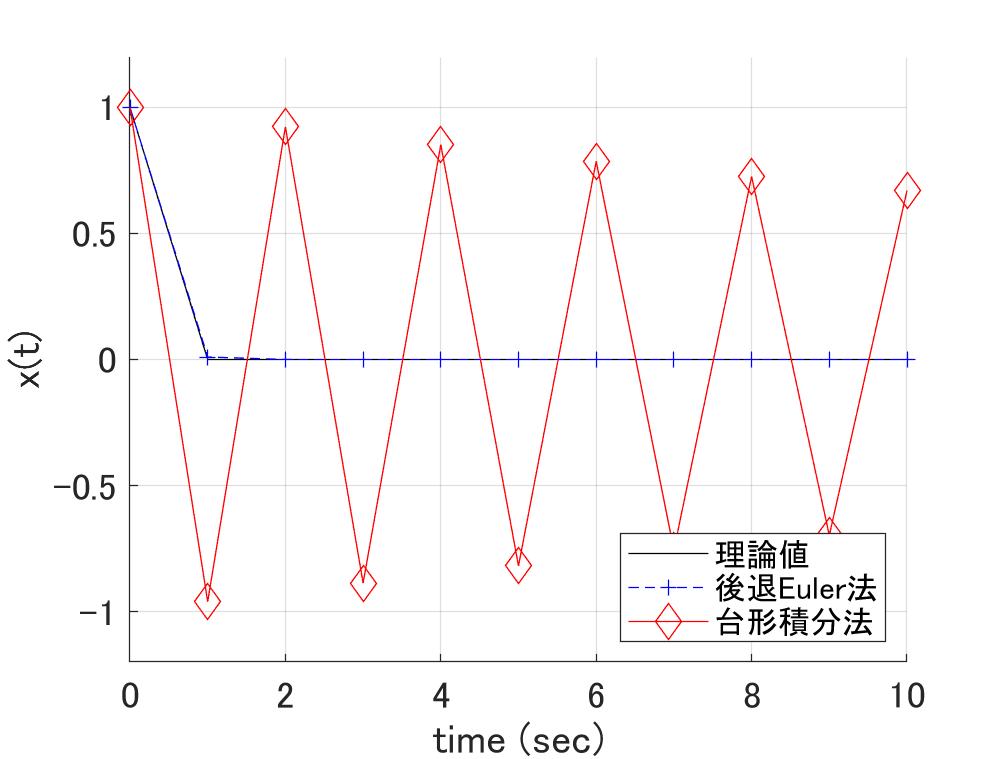
式\eqref{eq:diffExp_9}は厳密解なので、\(N=\infty\)まで頑張ればA安定のはずですが、たかだか\(N=10\)程度では、安定領域はかなり小さいです。ですが\(N=8\)を超えれば、まちの制御屋が意味のある安定領域とした領域を含みます。さらに\(N=10\)であれば^[6] … Continue reading、計算精度は\(h^{10}\)まで適合していて、なんとワンダフル。

• 

• 

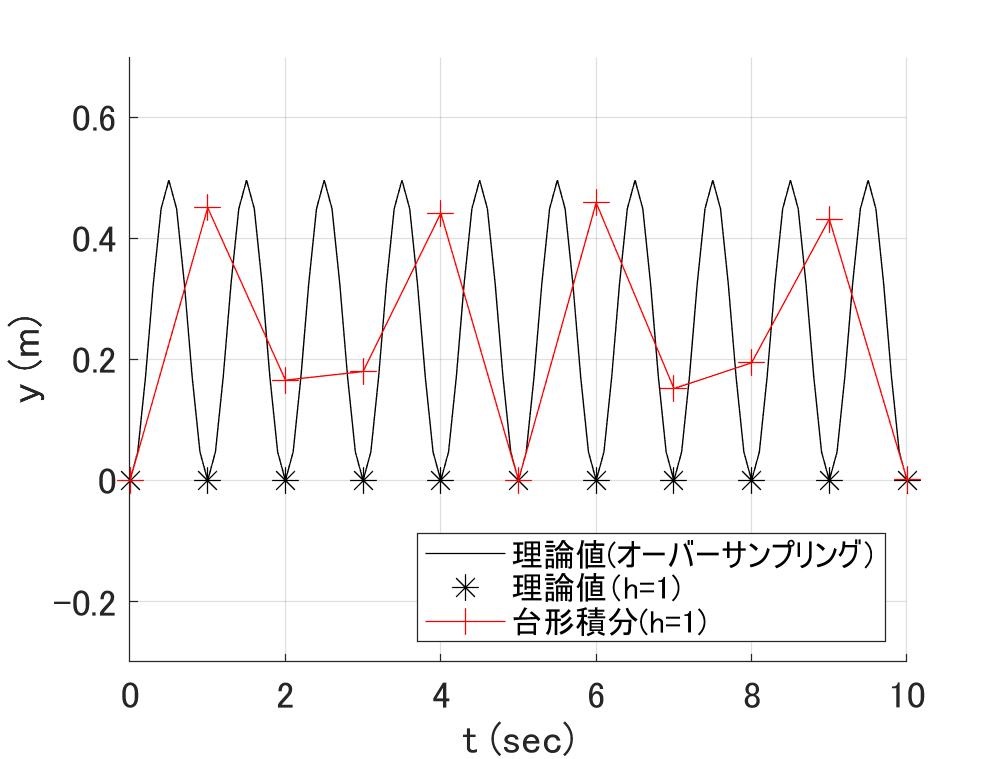
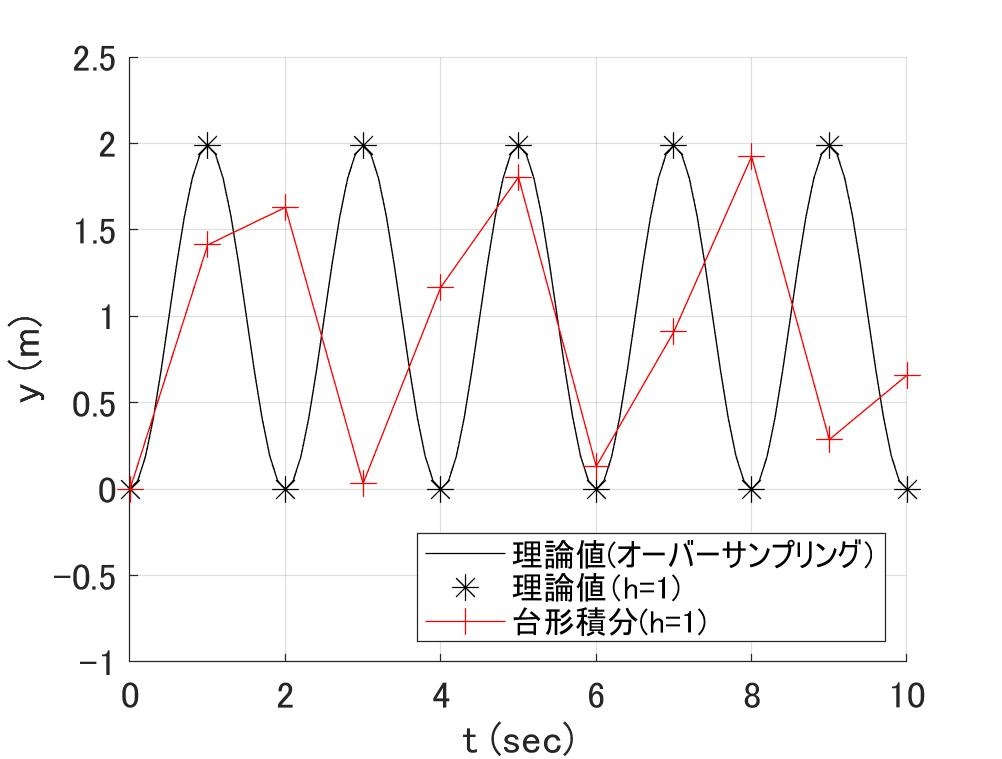
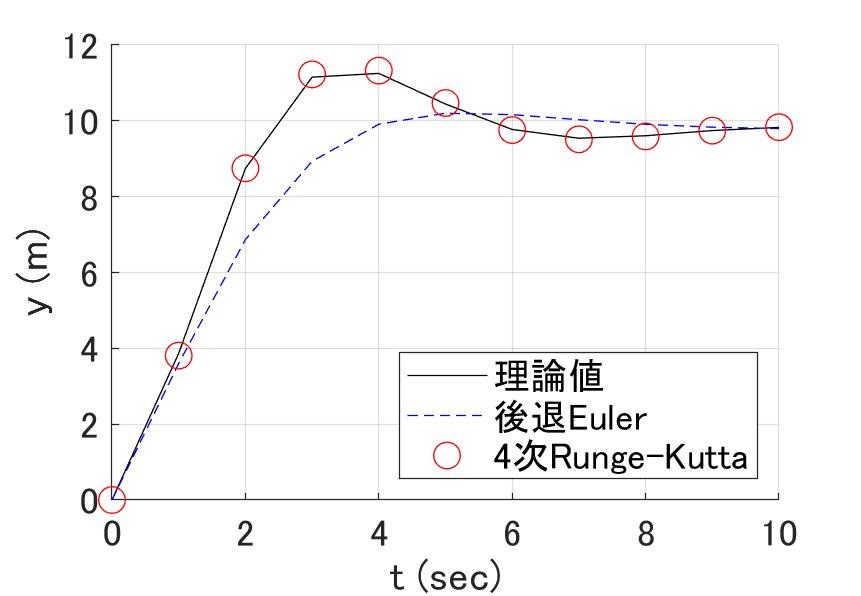
　図3a　\(h\lambda=\pm\pi i \)の場合　　　　図3b　\(h\lambda=-3\)（重根）の場合

さらに、式\eqref{eq:defMatExp_9}は順番に計算するだけなので、陽解放（Explicit-Method)です。反復計算は必要ありません。

をぉぉ、これこそがまちの制御屋が求めていた数値解法ではないですか？

この手法は、あまりに当たり前なのか、式\eqref{eq:diffExp_9}を計算するのがあまりに面倒なのか^[7] … Continue reading、線形に限定するのは数値計算屋の沽券にかかわるのか、教科書では見かけない手法です。
特に名称も決まっていないようです。
確かに式\eqref{eq:StateEq_9}をTaylor展開すれば得られるのでTaylor展開法と呼んでもよいのでしょうが、偏微分が出てこないTaylor展開法なんて。。。という気もします。

ですので、「N次指数関数法」と、呼ぶことにします。
あぁ、「N次指数関数法」に栄光あれ。

という、画期的な数値解法を掘り起こしたわけですが、
残念ながら、この手法は線形方程式限定です。

「線形方程式限定？　お客を選んだら、商売にならへんのや」
数値解法君の嘆く声が聞こえます^[8] … Continue reading。

やっぱ、任意関数でどうにかならんですかね？

前回、台形積分法に言いがかりをつけるにあたって、勢いで、
「台形積分法はL安定」ではない、とやったんですが、L安定とは、
「A安定でかつ、\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty}x_{i}=0\)」ですよね。\( Re(\lambda)\rightarrow-\infty\)なんて固有値を問題にしていいんでしょうか？虚軸方向は「Nyquist 周波数を超えたら意味はない」とブチかましておいて。

やはり、実数軸方向にも頃合いってもんがあるのでは？
ということで、前回の図4を再掲します。

• 

• 

図1a　\(h\lambda=-10\) 　　　　　　　　図1b　\(h\lambda=-100\)

計算しているのは、
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \qquad x(0)=1
\label{eq:Test}
\end{equation}
なので、ズバリ、
\begin{equation}
x(t) = e^{\lambda t}
\label{eq:AnSolution}
\end{equation}
が解析解ですが、例によって\(h=1\)で計算した場合、最初の1ステップ\((t=1)\)の値は
\(\lambda=-10\)の場合、\(e^{-10}=0.000045\)、
\(\lambda=-100\)の場合、\(e^{-100}=3.7201×10^{-44}\)
です。

ゼロの数を数えてくださいよ。計算初日（最初の1ステップ）で限りなくゼロです。過渡特性もなにもあったもんじゃない。
こんな固有値、計算する必要があるでしょうか？

という事で、実軸の固有値の限界を探ってみると、
\(h\lambda=-3\)の場合、\(e^{-3}=0.0498\)
\(h\lambda=-4\)の場合、\(e^{-4}=0.0183\)
\(h\lambda=-5\)の場合、\(e^{-5}=0.0067\)

\(h\lambda=-5\)までいけば、0.67%なので十分、2ステップ目からはさらにゼロに近づくことを考慮すれば、\(h\lambda=-4\)、\(h\lambda=-3\)でも大丈夫でしょう。

図2　\(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果

という事で、Stiffな方程式を計算するときに必要な安定領域は、虚数軸方向はNyquist 周波数ということで±3.14i、実数軸方向は-3の図3の領域で十分であり、必ずしもA安定である必要はない^[1] … Continue reading、というのが結論です。

図3　意味があると考える安定領域

「ですがね。計算しろよ！って渡された方程式が、都合の良い固有値を持ってる保証はないんですぜ、ダンナ」と数値解法君はおっしゃるでしょうね。

「しかしだ君。先ずは、安定領域内であれば、まともな精度で計算をやってあげるのが、君の誠というものではないかね、数値解法君？」

「安定であればどこでも、まともな計算精度」は少々厳しいので、まちの制御屋が意味があると断定した、実軸方向で\([-3,0]\)、虚軸方向で\([-\pi i,+\pi i]\)の範囲を安定領域に含み、この領域でまともな精度を持つ数値解法が欲しいところです。

4次のRunge-Kutta法は、残念ながら安定領域が足りません。陰解法に頼ろうにも、\(1<|h\lambda|\)の条件では、後退Euler法や台形積分法は適合次数が低く、Taylor級数の打ち切った項のタタリが怖すぎます^[2]虚軸方向で考察した、Taylor展開の収束の遅さは実軸でも同様。

これらを凌ぐ、安定領域が広く精度の高い手法はあるのでしょうか？
次回です。

参考文献
1: 「常微分方程式の数値解法　Ⅱ」 E. ハイラー G、ヴァンナー 三井　斌友　監訳　
2008年　シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド，
　　中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館

天下の台形積分法に言いがかりをつけるたぁいい度胸なんですが、つけます。
例によって、状態方程式
\begin{equation}
\frac{dX}{dt}=AX+Bf \\
\label{eq:StateEquation}
\end{equation}
\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
\:
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right]
\:
B= \left[
\begin{array}{c}
9.8 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
\(において、m=1　c=0\)で\(k=(2\pi)^2\)を\(h=1\)で計算すると、

図1　\(h=1\)で\(1Hz\)の波形を台形積分法で計算した結果

となります。なんか台形積分法の計算結果が変ですね。いや、それ以上に理論値が変です。よく見るとゼロから微動だにしません。

「君ねぇ、1Hzの振動波形だろう。サンプル周波数\(=1Hz (h=1) \)じゃ、Nyquist周波数を超えてるんだよ」

という偉い人の声が聞こえそうです。
そうなんですよね。台形積分法は（後退Euler法も）極めて広い安定領域を持ちますが、Nyquist周波数を超えた振動を与える固有値の場合、例え安定に計算できても、それはデータとして表現できないんで意味ないんじゃないか？

というのが第一のイチャモンです。

数値計算の教科書や論文は、「Stiffな方程式を計算するには、左半平面全てを含むA安定でなければならない」、という空気を漂わせるのですが、

Nyquist 周波数を超えた固有値の安定性なんか、無視してもいいんじゃないでしょうか？

「わかった、その件は不問にするから、とっとと立ち去り給え」　また偉い人の声が聞こえてきます。

しかし、これなんかどうでしょうか？　\(k=\pi^2\)でぴったりNyquist 周波数です。

図2　\(h=1\)で\(0.5Hz\)の波形を台形積分法で計算した結果

無い袖を振って、Nyquist周波数に入れたのに、つれないです。

そこで第２のイチャモンですが、台形積分法は\(h\)の2次の精度なのですが、2次では次数が足りてないんじゃないか？　です。

数値解法とTaylor展開で書きましたが、台形積分法の近似精度はTaylor展開の2次までです。
テスト方程式と呼ばれる
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \\
\label{eq:Test}
\end{equation}
の場合は、Taylor展開＝指数関数となり、Taylor級数を\(\infty\)までもっていけば厳密解となりますので（常微分方程式と状態方程式）、
\begin{equation}
　x_{i+1}= \left( 1+h\lambda+\frac{(h\lambda)^2}{2}+\frac{(h\lambda)^3}{3!} 　+…+\frac{(h\lambda)^\infty}{\infty !}\right)x_i
\label{eq:Exponential}
\end{equation}
という計算になります。
ですが、式\eqref{eq:Exponential}の級数をよく見ると\(1<|hλ|\)の場合、\(n\)乗すると、分子がどんどん大きくなって収束しないんじゃないかと心配になります。

ですが、分母が「！」で表される、発散させたら宇宙一の「階乗さま」ですから、収束することは間違いないです。

とは言え、\(1<|hλ|\)だと、収束するのに、かなりの次数が必要だということも事実です。
今は\( h\lambda=\pi i \)を問題にしていますが、めんどくせ~ので\(h\lambda=3\)とすると、台形積分法の場合、3次の項\(\frac{3^3}{3!}=\frac{27}{6} \)で打ち切ってますが、こんな大きな項を無かった事にしちゃっていいんでしょうか？
せめて１以下にならないと腰が落ち着かないなら、\(3^6=729\)に対し、\(6!＝720\)ですので\(h\)の7次、あるいはそれ以上まで項を積まないといけません。

さらにもう一つイチャモン。と言うより、おそらくこの特性は専門家の間では周知であり、”台形積分法イマイチだね～”という特性かと思います。

式\eqref{eq:Test}で\(h\lambda=-1\)として台形積分法で計算すると、こうなります。

図3　式\(\eqref{eq:Test}\)での計算結果（\(h\lambda=-1\)）

この条件なら、台形積分法は後退Euler法など寄せ付けませんが、

• 

• 

図4a　\(h\lambda=-10\) 　　　　　　　　図4b　\(h\lambda=-100\)

図4a、図4bのように\(h\lambda\)の実数部の絶対値を大きくすると、計算が振動的になる。
なんじゃらほいということで、式\eqref{eq:Test}の台形積分法の計算式を確認すると、
\begin{eqnarray}
　 x_{i+1}&=&x_i+\frac{h}{2} (\lambda x_i + \lambda x_{i+1} \\
　(2 – h\lambda) x_{i+1}&=& (2 + h\lambda )x_i \\
x_{i+1} &=& \frac{(2 + h\lambda)}{ (2 – h\lambda)} x_i
\label{eq:Trapezoidal}
\end{eqnarray}
ここで、\(Re(\lambda) \rightarrow -\infty \)だとしましょう。式\eqref{eq:Trapezoidal}は
\begin{equation}
　x_{i+1} =- x_i
\end{equation}
になりますから、プラスとマイナスをいったりきたりです。

このようにテスト方程式で、A安定でありかつ\( Re(\lambda)\rightarrow-\infty\)のとき、\(\lim_{i\to\infty} x_{i}=0 \)となる特性を、L安定と呼んでいるようで^[1]Wikipediaは英語版のみです。日本語の文献では見かけませんが、参考文献1にはしっかり記載されています、「台形積分法はL-Stableでないから。。。」^[2]ちなみに後退Euler法はL-Stableと知ったかぶるのがナウいようです（この場合はL-Stalbeね）

というわけで、台形積分法に対する言いがかりをまとめます。

１：台形積積分法はA安定（左半平面全体を安定領域とする）だが、Nyquist周波数を超えた領域は計算できても結果を正しく表現できないので、それほどのありがたみは無い。

２：\(1<|hλ|\)のような固有値は、2次や3次の計算アルゴリズムでは、かなり大きな誤差が生じるため、実用的ではない。

３：L安定でないから、実数部の絶対値の大きな固有値は安定領域であっても計算結果が振動的になってよろしくない。

言いたいことは、「台形積分法は、確かに広大な安定領域を持ってますが、意味のある固有値の範囲はごく一部だけ。一方2次という適合次数では、その意味のある固有値の多くで計算精度が足りない」ということです。

しかしながら、であっても、計算が発散してしまっては話にならないので、かつ非線形関数の場合、固有値を計算するのが面倒（かつL安定に関しては日本人は気が付いてない）なので、A安定である台形積分法は有用^[3] … Continue reading、というところですが、おそらく一番の魅力は、時間軸対象アルゴリズムなので、系のエネルギーが（計算誤差を除き）勝手に増減しないため、持続振動波形を長時間計算可能ということなんでしょう。
確かにこの点は買えます。

参考文献
1: 「常微分方程式の数値解法　Ⅱ」 E. ハイラー G、ヴァンナー 三井　斌友　監訳　
2008年　シュプリンガー・ジャパン
2: 「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド，
　　中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館

Taylor展開は厳密解だ^[1]∞回微分した項を含む級数が構成できればですが、これを計算すれば無問題、で話は終わりません。なんといっても知らない子\(\frac{d^k}{dt^k}f(t)\)がいます。これが解析的に得られているなら、そもそも発端の常微分方程式の解析解もオマケに付けてくれよぉ、なのて期待できません。
ですが流石に後世に名を残す人は違う、いい手があるのです。

いつもの常微分方程式
\begin{equation}
\frac{d}{dt}x(t) = f(x(t))
\label{eq:scalar}
\end{equation}
を2次までTaylor展開すると、
\begin{equation}
x(h + t_0)=x(t_0)+h f(x(t_0)) +\left. \frac{h^2}{2} \frac{d} {dt} f(x(t))\right|_{t=t_0}
\end{equation}
ですが、ここで、次のような変数を設定し、
\begin{eqnarray}
k_1 &=& f(x_i) \nonumber \\
k_2 &=& f(x_i+hk_1)
\end{eqnarray}
希望的観測かもしれないが、
\begin{equation}
x_i+h(a_1k_1 +a_2k_2 )= x_i + h f(x_i) +\left. \frac{h^2}{2} \frac{d} {dt} f(x(t)) \right|_{t=t_0}
\label{eq:Desired}
\end{equation}
となりゃせんだろうか？と考えます。

ならば、
\begin{equation}
a_1k_1 +a_2k_2 = f(x_i) +\left. \frac{h}{2} \frac{d} {dt} f(x(t)) \right|_{t=t_0}
\end{equation}
が成立しなければなりません^[2] … Continue reading。

式\eqref{eq:Desired}が任意の\(h\)で成立しない理由は無いならば、\(h=0\)でもよいので、
\begin{eqnarray}
a_1k_1 +a_2k_2 &=& a_1k_1 +a_2k_1=f(x_i) \nonumber\\
a_1+a_2&=&1
\label{eq:1stOrderCond}
\end{eqnarray}

一方、両辺を\(h\)で微分しても式\eqref{eq:Desired}は成立し、\(\frac {d}{dh}k_1=0\)なので
\begin{equation}
a_2\frac {dk_2}{dh}=\left.\frac{1}{2} \frac{d} {dt} f(x(t)) \right|_{t=t_0} \nonumber
\end{equation}

\(k_2=f(x_i+hf(x_i))\)である\(k_2\)と、\(x(t)\)を引数に持つ\(f(x(t))\)の微分には、合成関数の微分公式を適用して^[3]関数 \(y=f(u)　u=x(t)\)が共に微分可能な場合 \(\frac{df}{dt}=\frac{df}{du} \frac{du}{dt}=\frac{df}{du} \frac{dx(t)}{dt}\)が成り立つ、

\begin{equation}
a_2\frac {dk_2}{dh} =a_2\frac {dk_2}{dx}\frac{d(x_i+hf(x_i))}{dh} =\left.\frac{1}{2} \frac{f}{dx}\frac{dx(t)} {dt} \right|_{t=t_0} \nonumber
\end{equation}
ここで、\(h=0\)とすると、\(k_2=f(x)\)であるので、　
\begin{equation}
a_2\frac {df}{dx}f(x_i)=\frac{1}{2} \frac{df}{dx} f(x_i)
\end{equation}
以上より
\begin{equation}
a_2=\frac {1}{2}
\end{equation}
ならば式（\ref{eq:1stOrderCond}）より、
\begin{equation}
a_1=\frac {1}{2}
\end{equation}
なので、
\begin{eqnarray}
x_{i+1}&=&x_i+h(a_1k_1 +a_2k_2 ) \nonumber \\
&=&x_i+ \frac{h}{2} ( (f(x_i)+ f(x_i+hf(x_i) )
\end{eqnarray}
となる。

おお、これはHeun法（改良Euler法）ではないですか？

という事で、\(\frac{d}{dt}f(x)をf(x)\)で表すことが可能なことが解りました。

以上を大々的に拡張かつ一般化し、\(\frac{d^k}{dt^k}f(t)\)を\(f(x)\)の組み合わせで実現したものが、Runge-Kutta法です。
ですので、Heun法はRunge-Kutta法の一味ということになります。なお、以上はかなり簡略化しています^[4] … Continue reading。

4次のRunge-Kutta法は、\(f(x)\)だけを用いて、Taylor級数の\(h\)の4次の項まで等しくなるように工夫したものです。よくできています^[5] … Continue reading。

さて、ここで例によって、テスト方程式と呼ばれる
\begin{equation}
\frac{dx(t)}{dt}=\lambda x(t) \\
\label{eq:Test}
\end{equation}
を持ってくると、
\begin{equation}
\frac{d^2x}{dt^2}=\frac{\lambda x(t)}{dx} \frac{x(t)} {dt} = \lambda^2 x(t) \nonumber \\
\end{equation}
となって、
\begin{equation}
\frac{d^nx}{dt^n}=\lambda ^n x(t) \\
\label{eq:StateEquation_LIN}
\end{equation}
でいいんじゃないかと思いますが、これをTaylor展開に適用すれば、
\begin{equation}
x_{i+1}= \left( 1+h\lambda+\frac{(h\lambda)^2}{2}+\frac{(h\lambda)^3}{3!} 　+…+\frac{(h\lambda)^\infty}{\infty !}\right)x_i
\label{eq:Exponential}
\end{equation}
となり、以前にやった解析解となります^[6]常微分方程式と状態方程式。

式\eqref{eq:Test}の線形微分方程式をHeun法で計算すると、式\eqref{eq:Exponential}のhの2次の項までとなり、4次のRunge-Kutta法を適用してゴリゴリやれば、\(h\)の4次の項まで式\eqref{eq:Exponential}と一致します。

線形方程式の場合、n次のRunge-Kutta法はn次項の打ち切りの指数関数と同じなんですね。

ということで、少々遠回りをしましたが、いよいよ次回は
台形積分法に言いがかりをつけようと思います。

このBlogではStiffな常微分方程式の数値解法を扱っているのですが、多くの数値解法は、計算式の段階で近似式です。
それは、離散化した差分方程式だから、ではなく、差分方程式であっても厳密解を得る計算式はあるが、そうなっていない、という事です。

では差分方程式であっても厳密解を求める式とは、つまり\(x_{i+1}=x(t_0 + h)　　x_i=x(t_0)\)とした場合、\(x_iからx_{i+1}\)を厳密に求める式とはなんでしょうか？
それはTaylor展開です。

厳密な定義はWikipediaを参照してもらうとしてTaylorの定理-Wikipedia、
\begin{align}
x(h + t_0)=x(t_0)&+\left.h\frac{dx}{dt} \right|_{t=t_0} +\left. \frac{h^2}{2} \frac{d^2x} {dt^2} \right|_{t=t_0}\nonumber \\
&+…+ \left. \frac{h^\infty}{\infty!}\frac{d^\infty x}{dt^\infty} \right|_{t=t_0}= \sum_{k=0}^{\infty} \frac{h^k}{k!}\left.\frac{d^kx}{dt^k} \right|_{t=t_0}\\
\label{eq:TaylorExpantion}
\end{align}
が成立します^[1]厳密には、\(x(t)\)が無限に微分可能（＝\(C^\infty\)級）とかの条件が付くはずです。記号の使い方、あってますかね？

つまり、\(x_i=x(t_0)\)の値と、そこでの高次の導関数(\(\frac{d^k}{dt^k}x(t)\)等)があれば、\(x_{i+1}=x(t_0+h)\)が得られる、と、

対象とする常微分方程式を
\begin{equation}
\frac{d}{dt}x(t) = f(x(t))
\end{equation}
とすれば、
\begin{align}
x(t_0 + h)=x(t_0)&+ h f(t_0) + \left. \frac{h^2}{2} \frac{d f} {dt} \right|_{t=t_0}\nonumber\\
&+…+ \left. \frac{h^{k+1}}{(k+1)!}\frac{d^kf}{dt^k} \right|_{t=t_0}+…+ \left. \frac{h^\infty}{\infty!}\frac{d^\infty f}{dt^\infty} \right|_{t=t_0}
\label{eq:TylorExpantODE}
\end{align}
ですね。

しかしですね、「\(\frac{d^k}{dt^k}f(t)\)ってどこの子ですか？」と言いたいです。

そんな知らない子は無視すると、
\begin{eqnarray}
x(t_0 + h)&=&x(t_0)+h f(x(t_0)) \nonumber\\
x_{i+1}&=&x_i+h f(x_i)
\end{eqnarray}
ですね。これは前進Euler法です。

前進Euler法は1次の精度を持つ、あるいは１次で適合している^[2]他の文献の言い方は多少違いますが、参考文献にあげた「常微分方程式と微分方程式の数値解法」ではこの言い方ですとは、厳密解を与えるTaylor級数の\(h\)の1次の項まで一致している（そしてその後は無視している）という意味であることが解りました。

一方、式\eqref{eq:TylorExpantODE}は\(h\)がマイナスであっても通用するので、
\begin{eqnarray}
x(t_0 – h)&=&x(t_0) – h f(x(t_0)) \nonumber\\
x_{i-1}+h f(x_{i}) &=&x_{i} \nonumber\\
x_{i+1} &=&x_i + h f(x_{i+1})
\end{eqnarray}
後退Euler法と一致します。後退Euler法もやはり、１次でしか適合しない、ことが解りました。

では足して2で割る台形積分法はどうでしょうか？
展開の中心を\(x_{i+1/2}=x(t_0 + \frac{h}{2})\)として\(\pm{\frac{h}{2}}\)で式\eqref{eq:TylorExpantODE}を使い展開すると、
\begin{eqnarray}
x_{i+1}&=&x_{i+1/2}+\frac{h}{2} f(x_{i+1/2})+\frac{h^2}{2\cdot2^2} \frac{df}{dt}+ \frac{h^3}{6\cdot2^3} \frac{d^2f}{dt^2}+…\\
\label{eq:TrapezoidP}
x_{i}&=&x_{i+1/2}-\frac{h}{2} f(x_{i+1/2})+\frac{h^2}{2\cdot2^2} \frac{df}{dt} – \frac{h^3}{6\cdot2^3} \frac{d^2f}{dt^2}+…
\end{eqnarray}
式(6)ー式(7)を計算すると、\(h^2\)の項が消去されるので、
\begin{equation}
x_{i+1}-x_{i}= h f(x_{i+1/2}) +2\frac{h^3}{6\cdot2^3} \frac{d^3f}{dt^2}
\label{eq:TrapIMD1}
\end{equation}
ここで、さらに\( f(x_{i+1/2})\)を\(\pm{\frac{h}{2}}\)で展開し、
\begin{eqnarray}
f(x_{i+1})&=&f(x_{i+1/2}) + \left.\frac{h}{2} \frac{df}{dt} \right|_{x=x_{i+h/2}} +\frac{h^2}{2\cdot2^2}\frac{d^2f}{dt^3}+… \\
　f(x_{i})&=&f(x_{i+1/2}) -\left.\frac{h}{2} \frac{df}{dt} \right|_{x=x_{i+h/2}} + \frac{h^2}{2\cdot2^2}\frac{d^2f}{dt^3}+…
\label{eq:trapIMD2}
\end{eqnarray}
その和をとると
\begin{eqnarray}
　f(x_{i})+f(x_{i+1}) =2f(x_{i+1/2}) +\left.\frac{h^2}{2^2} \frac{d^2f}{dt^2}\right|_{x=x_{i+h/2}} +… \nonumber\\
f(x_{i+1/2}) =\frac{1}{2}\left(f(x_{i})+f(x_{i+1}) \right) -\left.\frac{h^2}{2^3} \frac{d^2f}{dt^2}\right|_{x=x_{i+h/2}} +…
\label{eq:TrapIMD3}
\end{eqnarray}
式\eqref{eq:TrapIMD3}を式\eqref{eq:TrapIMD1}に代入し、知らない子が関わっている\(h^3\)に続く項を無視すれば、
\begin{equation}
　x_{i+1}=x_i+\frac{h}{2} \left( f(x_{i}) +f(x_{i+1}) \right)
\end{equation}
という台形積分法の式が得られます。

\(h^3\)以上の項を切り捨てているので、2次の式ということになります。

以上、前進Euler法、後退Euler法、台形積分法の計算式がTaylor級数の一部と一致しているが、同時にTaylor級数のかなり多くの項を無視していることがわかりました。ですがが、無視されるのは寂しいので、もっと多くの項まで面倒を見ることはできないでしょうか？

そのためには、知らない子\(\frac{d^k}{dt^k}f(t)\)をなんとかしなくてはいけません。

参考文献
「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド　共著，中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館
「微分方程式による計算科学入門」 　　　三井　斌友　小藤　俊幸　斉藤　善弘 2004年共立出版

Stiffな常微分方程式を計算するのは容易ではない。

これが前回の結論ですが、出来ないわけではない。いやStiff専用の数値解法が存在します。
\begin{equation}
\frac{dx(t)}{dt} = \lambda x(t)
\label{eq:scalar}
\end{equation}
という常微分方程式を
\begin{equation}
　\frac{dx}{dt} \simeq \frac{x_{i+1}-x_i}{h} =\lambda x_i \\
\hspace{30mm} x_i=x(t_0) \quad　x_{i+1}=x(t_0 +h)
\end{equation}
とするのが前進Euler法でしたが、
\begin{equation}
　\frac{dx}{dt} \simeq \frac{x_{i}-x_{i-1} } {h} =\lambda x_i \\
\hspace{30mm} x_i=x(t_0) \quad x_{i-1}=x(t_0 – h)
\end{equation}
というのもアリなんじゃないか？という疑問が生じます。
これが後退Euler法です。

式を変形すると、その差が解りやすくなります。前進Euler法は
\begin{equation}
x_{i+1}=x_i + h\lambda x_i
\label{eq:FEequation}
\end{equation}
ですが、後退Euler法は
\begin{equation}
x_{i+1}=x_i + h\lambda x_{i+1}
\label{eq:BEequation}
\end{equation}
です。

図1　後退Euler法と前進Euler法の違い

式\eqref{eq:FEequation}と式\eqref{eq:BEequation}の差は微妙ですが、その意味するところは図1のようになります。

そしてこの微妙な差は、計算安定領域に決定的な差を生じます。
つまり、前進Euler法の安定領域は、

\begin{equation}
|1+h\lambda|<1
\label{eq:FEStableCond}
\end{equation}
ですが、後退Euler法の安定領域は
\begin{equation}
\frac{1}{|1-h\lambda|}<1
\label{eq:BEStableCond}
\end{equation}
となり、左半平面が完全に含まれます。なお、このような特性をA安定（A-Stable）と言います。

• 

• 

つまり、連続系の式\eqref{eq:scalar}が発散しないなら、式\eqref{eq:BEequation}の後退Euler法も”絶対に”発散しないので、Stiffだろうが、固有値が遥か彼方だろうが、安定に計算することができます。

ですが、これで解決なんでしょうか？

まず、後退Euler法の問題点として、式\eqref{eq:BEequation}をよく見ると、左辺の\(x_{i+1}\)を得るために右辺の\(x_{i+1}\)を必要とします。穏やかでないですね。

このような方程式をImplicit-Method（陰解法）と言い、単純に右から計算して左に代入というわけにはいきませんから、適当な初期値を\(x_{i+1}\)に与え、少しずつ値を追い込んでいく、ニュートン法に代表される収束計算が必要となります ^[1]この例のような線形方程式の場合は、左辺へ移行して、除算または逆行列で計算できますが。

これに対して前進Euler法のような\(x_{i+1}\)を得るには\(x_{i}\)しか必要としない手法はexplicit-Method（陽解法）と呼ばれ、右から左へチャンチャンと計算できます。

後退Euler法のもう一つの問題点として、近似精度が1次であり4次のRunge-Kutta法などに比べ、計算精度が大幅に見劣りするという事があります。

状態方程式
\begin{equation}
\frac{dX}{dt}=AX+Bf \\
\label{eq:StateEquation}
\end{equation}

\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
\quad
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right]
\quad
B= \left[
\begin{array}{c}
9.8 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
において、\(m=1　k=1　c=1\)を\(h=1\)で計算すると、

図4　4次のRunge-Kutta法と後退Euler法の$h=1$における計算結果

\(h=1\)というかなり大きめの計算ステップであっても、4次のRunge-Kutta法なら、ほぼ理論値ですが、後退Euler法は、”しかたねぇか”、という感じになります。

そこで、もう一度図1をじ～っと見ると、前進Euler法と後退Euler法を足して2で割ると、いい感じじゃね？　という事に気付きます。

そこで、
\begin{equation}
2x_{i+1}=2x_i + h\lambda x_i + h\lambda x_{i+1}
\end{equation}
これを変形して、
\begin{eqnarray}
2x_{i+1}-h\lambda x_{i+1}=2x_i + h\lambda x_i \nonumber\\
x_{i+1} = \frac{2+h\lambda }{2-h\lambda} x_{i}
\end{eqnarray}
この手法は、台形積分法（Trapezoidal-Rule)と呼ばれます^[2] … Continue reading。
安定領域は
\begin{equation}
\left| \frac{2+h\lambda }{2-h\lambda} \right|<1
\end{equation}
となり、これを図示すると、

図5　台形積分法の安定領域

なので、「Oh!　ぴったり左半平面！」　必要にして十分とはまさこの事、と狂喜します。

さらに、その計算精度は\(h\)の2次とされており、時系列で計算してみると、

図6　4次のRunge-Kutta法と台形積分法の\(h=1\)における計算結果

かくして安定領域は必要にして十分、計算精度もそこそこある、ということで、Stiffな方程式に対する、有力な計算手法が得られました^[3]「いや俺はGear法を信じる」、という方もいるでしょう。この件も後でキッチリオトシマエを付けます。

ですが、ここで終わればこのホームページを作ろうとは思わなかったわけで、やはり問題があるのですよ。
台形積分法もImplicitなので、計算するのはやっかいなのですが、それ以上にImplicit-Method全般に言えるような、問題というか、イチャモンがあると思っています。

ですが、その前に、前進／後退Euler法は1次、台形積分法は2次の精度とは何でしょうか？

まずは、その点を明らかにしておきましょう。

参考文献
「常微分方程式と微分方程式の数値解法」 U.M. アッシャー，L.R.ペツォルド　共著，中村　眞理雄　監訳　嘉村友作・三ツ間　均　共訳　2006年　培風館
「微分方程式による計算科学入門」 　　　三井　斌友　小藤　俊幸　斉藤　善弘 2004年共立出版

常微分方程式で数値計算の教科書を見ると、ファン デル ポール(van der Pol)方程式^[1]こんな式らしいです。\(\frac{d^2x}{dt^2}+\mu(x^2-1)\frac{dx}{dt}+x=0 \)とかを例にしますが、まちの制御屋には縁のないものです。

まちの制御屋がガップリ四つに組むのは、線形運動方程式です。
図1の様なものを記述する方程式です。

図1　基本的な機械機構の図

機械システムとしては一丁目一番地の運動方程式で、
\begin{equation}
m\frac{d^2}{dt^2}y(t)+c\frac{d}{dt}y(t)+ky(t) = mg
\label{eq:MotionEquation}
\end{equation}
と記述できますが、実は、これが手強い。

これを、状態方程式とすると、
\begin{equation}
\frac{dX}{dt}=AX+Bf
\label{eq:StateEquation}
\end{equation}

\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right] \quad
B=\left[
\begin{array}{c}
1 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
となりますが、これを、最終兵器と名高い4次のRunge-Kutta法で計算しようとしても、できなかったりします。

図2で\(m=1\)　\(k=1\)　の場合に、ダンピング係数\(c\)を変えて、\(h=0.5\)で計算した場合の結果ですが、\(c=1\)では、もっともらしい結果が出ます。

さすがはRnge-kutta法だ、\(h\)が大きくてもそれなりに計算をする、のですが、\(c=6\)にすると、あっさり発散します。

図2　式\eqref{eq:StateEquation}におけるダンピング係数cと時間応答の関係

「変化が速いもの計算するには、計算ステップを細かくしなければらない」、というのは猫でも解ることですが、

\(c=1\)に比べて\(c=5\)の場合は、図2のように”動きが遅く”、\(c=6\)の場合はさらに遅くなるはずですが、途中であらぬ方向に発散して行きます。

これがStiffです。

種明かしをしましょう。

式\eqref{eq:StateEquation}の状態方程式は固有値分解、すなわちある正則行列\(P\)を用いて対角行化して連立方程式とすることができます。

\begin{equation}
\frac{d}{dt}Z=\Lambda Z+P^{-1}B f
\label{eq:DiagonalEqation}
\end{equation}
\begin{eqnarray}
\lambda := \left[
\begin{array}{cc}
\lambda_1 & 0 \\
0 & \lambda_2 \\
\end{array}
\right] = P^{-1}AP
\qquad
Z := \left[
\begin{array}{c}
z_1 \\
z_2 \\
\end{array}
\right] = P^{-1}X \nonumber
\end{eqnarray}

結果、以下の独立した2個の常微分方程式が得られます。
\begin{eqnarray}
\frac{d}{dt}z_1 = \lambda_1 z_1 + b_1 \nonumber\\
\frac{d}{dt}z_2 = \lambda_1 z_2 + b_2
\label{eq:SimulEquation}
\end{eqnarray}
\begin{equation}
\hspace{30mm}
\left[ \begin{array}{c}
b_1 \\
b_2 \\
\end{array}\right]
:= P^{-1}Bf \nonumber
\end{equation}
つまり、式(\ref{eq:StateEquation})を計算するとは、式(\ref{eq:SimulEquation})の連立方程式を同時に計算するという事なのです。

\(c=1、c=2、c=5\) 及び\(c=6\)とダンピング係数を変化させたときの固有値\(\lambda\)を計算し、hを乗じた値をプロットすると、図3になります。

図3　ダンピング係数\(c\)と固有値の関係

「〇」でプロットしたのがc=1のときの固有値ですが、c=2で実軸上の「＋」でプロットした場所に固有値（この場合は重根）が移動し、その後は実軸の上を原点に近い方向と、原点から遠い方向に分離していきます。
そしてダンピング係数\(c\)をたかだか6倍した程度で、「広くなって安心ね」の4次のRunge-kutta法の安定領域を超えていきます。

このように、原点に近い（遅い）固有値と、原点から遠い（速い）固有値を併せ持つ方程式をStiffな（＝硬い）方程式と呼びます。運動方程式を構成したとき、”硬い”機械系をモデル化したときに発生した事が由来とされています^[2]この”硬い”方程式が、ここでの例の様にダンピング過剰なのか、バネ定数が大きすぎたのかはわかりません。どなたかご存知でしょうか？。

Stiffな方程式の場合、原点から遠い固有値も安定領域に入るようにステップサイズを選ばなければなりませんが、それは、緩やかな（鈍い）運動を与えている原点に近い固有値に対しては、小さすぎることにもなりかねません

実務では、ダンピング力が速度に応じて変わるような非線形特性を組込みことがありますが、摩擦力を模擬するために、速度\(=0\)付近ではダンピング係数を大きく取る等のモデルを作ると、そこで計算が発散して一歩も先に進めない、というのはシミュレーションあるあるのネタ。

そうなると、ステップサイズ\(h\)を極端に小さくする意外に手がなくなり、計算時間がやたらと長くなります^[3] … Continue reading。

「計算に時間がかかるから、その間は休憩」、なんてやっている部下をお持ちの方、それは計算の仕方が悪いんですよ。

ということで、次回は「４：Stiff対応の数値解法」です。

常微分方程式で解析解が得られるのは、運が良いからだ、というのが定説ですので、一般的には数値計算に頼ることになりますが、そう言うと、「計算精度はどうなの？」という話になります。

ですが、制御屋は精度より、安定性を気にします。

\begin{equation}
\frac{dx(t)}{dt} = \lambda x(t)
\label{eq:scalar}
\end{equation}
という常微分方程式の解は、以前書いた「１：常微分方程式と状態方程式」より
\begin{equation}
x(t) = e^{\lambda t} x(0)
\end{equation}
ですが、ここで複素数である\(\lambda\)の実数部が正であると、\(e^{\lambda t}\)は、\(t\)が増えるにつれ、正に指数関数的に増加するので、無限大まで突っ走るしかありませんが、逆に実数部が負であれば、漸近的に零に収束し、何らかの解が得られることになります

一方、数値計算を行う場合ですが、例えば式(\ref{eq:scalar})の微分演算を、微小な値である\(h\)の間の差であると、かなり大雑把に考えれば、
\begin{equation}
\frac{dx}{dt} \simeq \frac{x_{i+1}-x_i}{h} =\lambda x_i
\end{equation}
\begin{equation}
x_i=x(t_i) \quad x_{i+1}=x(h+t_i) \nonumber
\end{equation}
となり、
\begin{equation}
　　　x_{i+1}=x_i+h\lambda x_i
　　　\label{eq:F_Euler}
\end{equation}
ですので、\(x_i\)から\(x_{i+1}\)を順次計算することができます。これが前進Euler法と呼ばれる数値計算手法です。

ここで式\eqref{eq:F_Euler}は
\begin{equation}
x_{i+1}=(1+h\lambda) x_i
\end{equation}
ですので、\((1+h\lambda)\)の絶対値が\(１\)より大きければ、\(x_i\)に対して\(x_{i+1}\)は常に大きくなるので、やはり無限大まで突っ走ってしまいます。

つまり、前進Euler法は\(h\lambda\)が

\begin{equation}
|1+h\lambda|<1
\label{eq:FEStableCond}
\end{equation}
を満たさない限り、計算が発散するのです。

式(\ref{eq:FEStableCond})の\(λ\)は複素数を認めますので、式(\ref{eq:FEStableCond})を図示すると、図1の複素平面内の単位円の内側が安定領域という事になります。

図1　前進Euler法の安定領域

元々の微分方程式である式\eqref{eq:scalar}では、\(\lambda\) の実数部が負であれば安定でしたが、前進Euler法の場合は、虚数部も含めて所定の範囲内でなければならない、と条件が厳しくなります。

しかしながら、\(h\)を掛けているので、\(\lambda\) が大くてはみ出しそう、という場合は\(h\)を小さくして対抗することができます。
その結果、「計算が発散する？　ならステップサイズ(\(=h\))を小さくしろ！」という声があちこちから聞こえることになります。

さて、話は変わりますが、「改良Euler法(Improved Euler Method)」というものがあります^[1]ここでいう改良Euler法は陽的台形法の事ですが、中点を用いる修正Euler法(Modified Euler … Continue reading。

前進Euler法ではあまりに大雑把なので、”改良”したわけですが、
\begin{equation}
x_{i+1}=x_{i}+{\frac {1}{2}}h(f(t_{i},x_{i}) + f(t_{i+1},x_{i}+hf(t_{i},x_{i})) )
\label{eq:HeunMethod}
\end{equation}
という計算式で、計算誤差は\(h\)の2乗に応じて減少する事になっており、常微分方程式を構成する関数を２回計算するだけで、誤差が大幅に小さくなるオトクな計算法ですが、これを式\eqref{eq:scalar}に適用すると、
\begin{eqnarray}
x_{i+1}&=&x_{i}+{\frac {1}{2}} h (\lambda x_{i} + \lambda (x_i + h \lambda x_i) )\nonumber \\
&=&x_{i}+ h \lambda x_{i} + {\frac {1}{2}} (h \lambda)^2 x_i
\end{eqnarray}
ですので、
\begin{equation}
\left|1+h\lambda+\frac{(h\lambda)^2}{2} \right|<1
\label{eq:HeunStableCond}
\end{equation}
が安定条件となり、図示すると、

図2　改良Euler（Heun)法の安定領域

前進Eulerより安定領域が広がりました。数値計算は、計算手順を変えれば精度だけでなく、安定性も変わるのです。

こうなれば、あとは\(h\)で頑張れば、どんな\(\lambda\)が来ても大丈夫・・・ とはなりません。
この図ではわかりにくいですが、\(\lambda\)が虚軸上にあるとhをどんなに小さくしても、厳密には安定領域には入らないのです。
\(\lambda\)が虚軸上にあるというのは、減衰のない振動が持続するケースですが、その場合は、改良Euler法はいかがなものか？　となります^[2]をそれなりに小さくすれば、安定領域にかなり近いところになり、徐々に発散するため、実用的にはOK、という場合もあります。

ここで、真打の登場です。

常微分方程式の計算といえば、4次のRunge-Kutta法に止めを刺す、と長らく言われておりました。
\begin{eqnarray}
x_{i+1}&=&x_{i}+{\frac {h}{6}}(k_1+2k_2 + 2k_3+k_4)\nonumber \\
k_1&=&f(t_{i}\; , \; x_{i})\nonumber \\
k_2&=&f(t_{i}+\frac{h}{2}\; , \; x_{i}+\frac{h}{2}k_1)\nonumber \\
k_3&=&f(t_{i}+\frac{h}{2}\; , \; x_{i}+\frac{h}{2}k_2)\nonumber \\
k_4&=&f(t_{i}+h\; , \; x_{i}+hk_3)
\end{eqnarray}

4次のRunge-Kutta法は、その名のとおり\(h\)の4次の精度を持ち^[3]Taylor展開で与えられる厳密解に対し、\(h\)の4次の項まで一致する、関数を4回計算すれば4次の精度が得られる、オトクでお値打ちな計算法で、さらに安定条件は
\begin{equation}
\left|1+h\lambda+\frac{(h\lambda)^2}{2} + \frac{(h\lambda)^3}{2\cdot3} + \frac{(h\lambda)^4}{4!}　\right|<1
\label{eq:ClassicRKStableCond}
\end{equation}
です。

4次のRunge-Kutta法の安定領域

おおっ！かなり広い安定領域。しかも虚軸も含まれているではないですか！　これで、もう安心、あとは何があっても\(h\)で頑張る、。。。という時代もあったのですが、現在では、いやこのBlogではそれは許しません。

なぜなら、Stiffに弱いから

ということで、次回に続きます。

常微分方程式とは

Wikipediaによれば
「常微分方程式（じょうびぶんほうていしき、英: ordinary differential equation, O.D.E.）とは、数学において、未知関数とその導関数からなる等式で定義される方程式である微分方程式の一種で、未知関数が本質的にただ一つの変数を持つものである場合をいう」常微分方程式 – Wikipedia
とあります。

完全に奥歯にモノが挟まってますが、各方面のご指摘を恐れなければ、
\begin{equation}
　\frac{dx(t)}{dt} = f(t,x(t))
　　\label{eq:Scalar}
\end{equation}
の形の微分方程式を常微分方程式とする、でいいでしょう。

つまり、ただ一つの変数\(t\)を持つ未知関数\(x(t)\)とその導関数からからなる微分方程式です。
さらに、例えば、
\begin{eqnarray}
x_2 &=& \frac{dx_1}{dt} \nonumber \\
x_3 &=&\frac{dx_2}{dt} = \frac{d^2x_1}{dt^2} \nonumber
\end{eqnarray}

とすることで、高階の導関数を\(X=[x_{1},x_{2}, … ,x_{n}]^t \)ベクトルの要素とし、ベクトル関数 \(F(t,X(t))\)を用いて、
\begin{equation}
\frac{dX(t)}{dt} = F(t,X(t))
\label {eq:Vector}
\end{equation}

としておけば、微分の微分の…といった方程式も扱えるので、
これを基本形としましょう。

制御屋をやっていると、この常微方程式と付き合いが避けられないのですが、なにより、現代制御（といっても50年前の理論ですが）の大黒柱である状態方程式（State Space Equation）が常分方程式そのものですね。式\eqref{eq:Vector}を線形に限定したものが、次の状態方程式です。
\begin{equation}
\frac{dX(t)}{dt}=AX(t)+BU(t)
\label {eq:StateEq}
\end{equation}

とある状態変数^[1]”とある状態変数”とは何ぞや？というのは、意外に深いので流してくださいのベクトルである状態変数ベクトル\(X(t)\)と外部から与えられる変数である入力ベクトル\(U(t)\)とを、行列ＡおよびＢを用いて、線形式にしたものが、\(X(t)\)の導関数に等しい、という式になります。

式(\ref{eq:Vector})のような一般形で\(X(t) \)を解析的に求めるのは困難ですが、式(\ref{eq:StateEq})の状態方程式は有難いことに解析解が知られています。

とりあえず\(U(t)\)ベクトルを無視して、スカラー式で考えるなら、
\begin{equation}
\frac{dx(t)}{dt}= \lambda x(t)
\label {eq:testEq}
\end{equation}
ですので、これは
\begin{equation}
x(t) = x(0)e^{\lambda t}
\end{equation}
です。

こうなるように\(e\)を仕込んである、いや以下に定義してあるので、
\begin{equation}
e^{\alpha }:=1+\alpha+\frac{\alpha^2}{2!}+…+\frac{\alpha^\infty}{\infty!}=\sum_{k=0}^{\infty} \frac{\alpha^k}{k!}
\label{eq:expDef}
\end{equation}

そうなります。式\eqref{eq:expDef}において\(\alpha=\lambda t \)とすれば、式(\ref{eq:testEq})を満たすはずです。

なお、\(x(0)\)は\(t=0\)における初期値ですね。常微分方程式を解くことは初期値問題とも呼ばれ、初期値が無いと解けない、いや初期値さえあれば解けるという事になっています。

では、式\eqref{eq:StateEq}はどうか？　
これは、やはりこう仕込みます。Wikipediaでは行列指数関数(Matrix Exponential Function)と呼ばれてるようですが、定数である\(e\)の行列乗という、なんだか解らない数を、ためらうことなく定義して、立ち去ります。

\begin{equation}
e^{A}:=I+A+\frac{A^2}{2!}+…+\frac{A^\infty}{\infty!}= \sum_{k=0}^{\infty} \frac{A^k}{k!}
\label{eq:defMatExp}
\end{equation}

コイツさえあれば、
\begin{equation}
X(t)=e^{At} X(0)
\end{equation}

です。ちなみに式\eqref{eq:defMatExp})は制御の分野では状態遷移行列(State Transition Matrix)と呼ばれています。

さて、ここで置き去りにした\(U\)ベクトルを思い出すと、式\eqref{eq:StateEq}の状態方程式は
\begin{equation}
X(t)=e^{A (t-t_o)}X(t_o) + \int_{t_0}^{t} e^{A(t-\tau)} BU(\tau) d\tau
\label{eq:resoSolution}　
\end{equation}
と解けるとのよし。

なんか解ったような解らないような、感じです。　
そこで、「実は\(U(\tau)\)は区間\([t、t_0]\)で定数です！」と衝撃の告白を行います。
ならば\(BU\)は積分の対象外ですので、

\begin{equation}
X(t)=e^{A (t-t_o)}X(t_o) + \int_{t_0}^{t} e^{A(t-\tau)} d\tau BU
\label{eq:resoSolution2}
\end{equation}
です。

これならば、
\begin{eqnarray}
X(t)&=&e^{A (t-t_o)}X(t_o) +　\int_{t_0}^{t} e^{A(t-\tau)} d\tau BU\nonumber \\
&=&e^{A (t-t_o)}X(t_o) +　e^{At} \int_{t_0}^{t} e^{A(-\tau)} d\tau BU \nonumber \\
&=&e^{A (t-t_o)}X(t_o) +　e^{At} \left (-e^{-At} +e^{-At_0} \right)A^{-1} BU\nonumber \\
&=&e^{A (t-t_o)}X(t_o) +　 \left (e^{A(t-t_0)} – I \right)A^{-1} BU
\label{eq:resoSolution3}
\end{eqnarray}
ですね^[2]状態遷移行列は、その定義式\eqref{eq:defMatExp}よりA行列で右から除しても左から除しても同じ。

しかし、「\(U\)が区間\([t、t_0]\)で定数は許せない！」と冷たく拒絶されるかもしれません。
そこで、すごく小さい\(h\)の間だけ、つまり「\(U\)は区間\([h+t_0、t_0]\)の間だけ定数です」、と許しを請います。
\begin{eqnarray}
X(h+t_0)=e^{A h}X(t_0) +(e^{A h} – I )A^{-1} BU_{t_0}
\end{eqnarray}
です。

さらに、「実は\(X(t_0)\)は離散数列\(X\)の\(i\)番目の数\(X_i\)で、\(X(h+t_0)\)は\(X_{i+1}\)でした」と、たたみかければ
\begin{equation}
X_{i+1}=e^{A h}X_i + (e^{A h} – I )A^{-1} BU_i
\label{eq:diffExp}
\end{equation}
となり、\(h\)をかなり小さくすれば、任意のtに関する\(X(t)\)（に近い）値が得られます^[3]ですが、実際に式\eqref{eq:diffExp}を計算するのは、一筋縄ではいきません。それはまた後ほど。

---

参考文献
「微分方程式による　計算機入門」三井　斌友　小藤　俊幸　齊藤　善弘　2004年　共立出版社
「システム制御理論入門」 　　　　小郷　寛　美多　勉　　1979年　実教出版社