常微分方程式で数値計算の教科書を見ると、ファン デル ポール(van der Pol)方程式[1]こんな式らしいです。\(\frac{d^2x}{dt^2}+\mu(x^2-1)\frac{dx}{dt}+x=0 \)とかを例にしますが、まちの制御屋には縁のないものです。
まちの制御屋がガップリ四つに組むのは、線形運動方程式です。
図1の様なものを記述する方程式です。
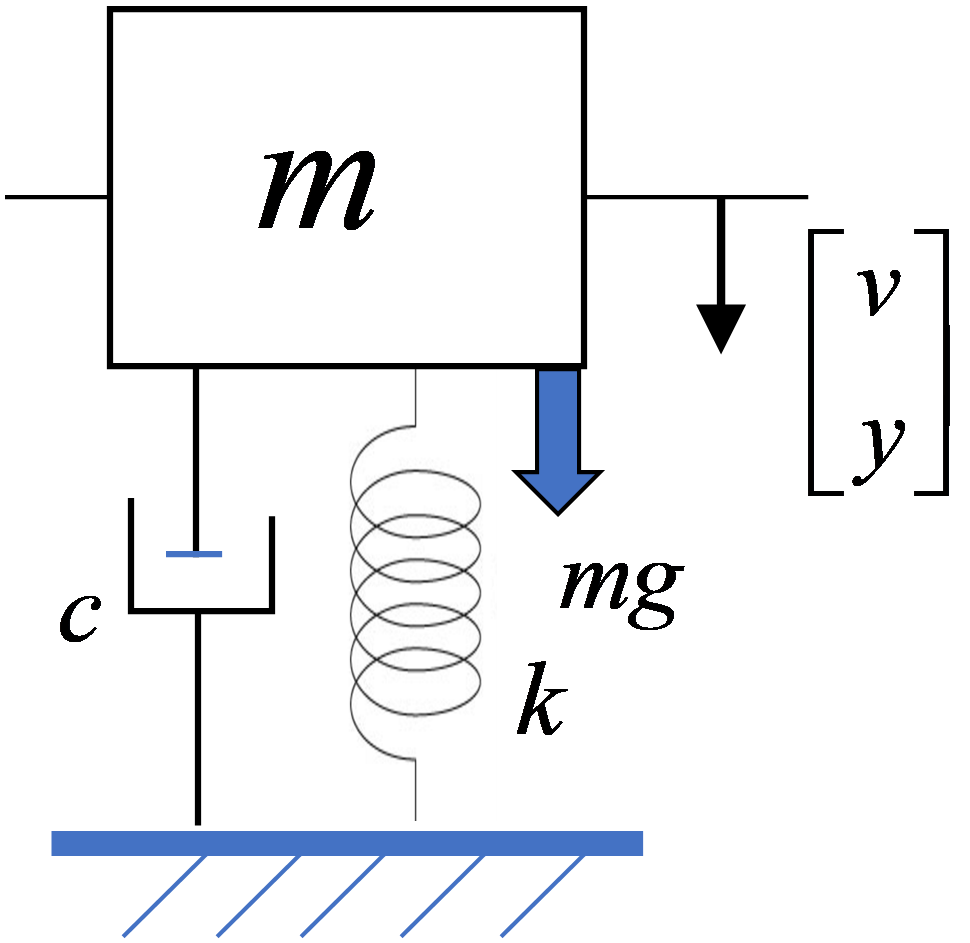
図1 基本的な機械機構の図
機械システムとしては一丁目一番地の運動方程式で、
\begin{equation}
m\frac{d^2}{dt^2}y(t)+c\frac{d}{dt}y(t)+ky(t) = mg
\label{eq:MotionEquation}
\end{equation}
と記述できますが、実は、これが手強い。
これを、状態方程式とすると、
\begin{equation}
\frac{dX}{dt}=AX+Bf
\label{eq:StateEquation}
\end{equation}
\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right] \quad
B=\left[
\begin{array}{c}
1 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
となりますが、これを、最終兵器と名高い4次のRunge-Kutta法で計算しようとしても、できなかったりします。
図2で\(m=1\) \(k=1\) の場合に、ダンピング係数\(c\)を変えて、\(h=0.5\)で計算した場合の結果ですが、\(c=1\)では、もっともらしい結果が出ます。
さすがはRnge-kutta法だ、\(h\)が大きくてもそれなりに計算をする、のですが、\(c=6\)にすると、あっさり発散します。
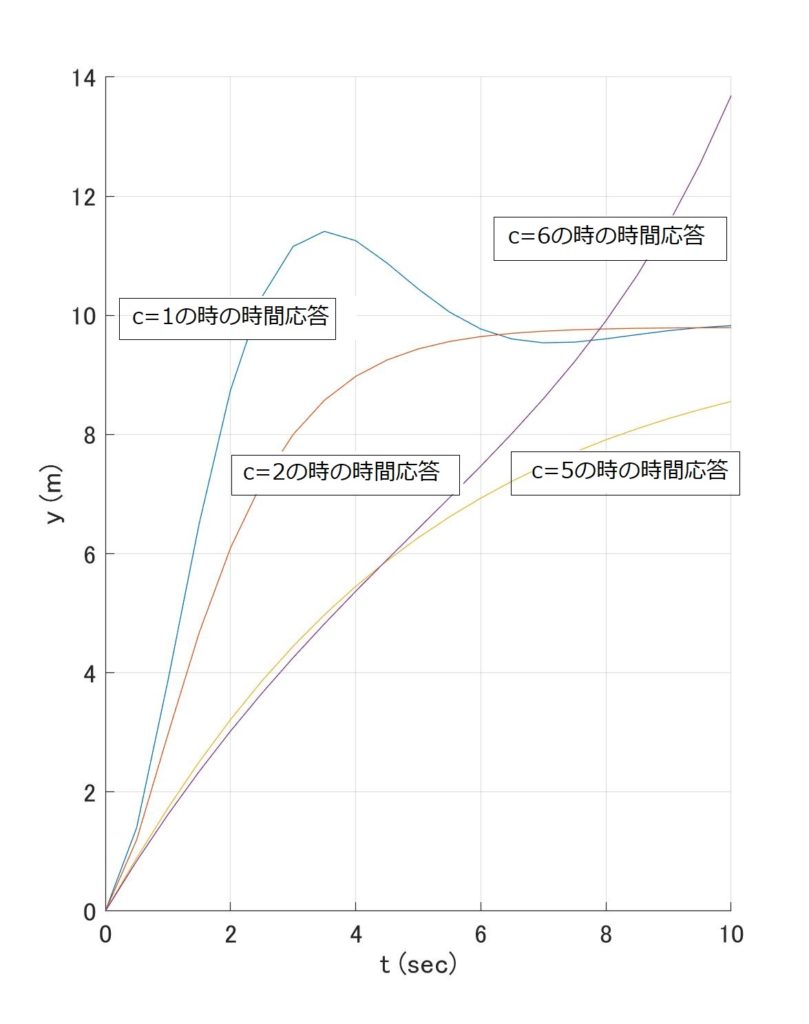
図2 式\eqref{eq:StateEquation}におけるダンピング係数cと時間応答の関係
「変化が速いもの計算するには、計算ステップを細かくしなければらない」、というのは猫でも解ることですが、
\(c=1\)に比べて\(c=5\)の場合は、図2のように”動きが遅く”、\(c=6\)の場合はさらに遅くなるはずですが、途中であらぬ方向に発散して行きます。
これがStiffです。
種明かしをしましょう。
式\eqref{eq:StateEquation}の状態方程式は固有値分解、すなわちある正則行列\(P\)を用いて対角行化して連立方程式とすることができます。
\begin{equation}
\frac{d}{dt}Z=\Lambda Z+P^{-1}B f
\label{eq:DiagonalEqation}
\end{equation}
\begin{eqnarray}
\lambda := \left[
\begin{array}{cc}
\lambda_1 & 0 \\
0 & \lambda_2 \\
\end{array}
\right] = P^{-1}AP
\qquad
Z := \left[
\begin{array}{c}
z_1 \\
z_2 \\
\end{array}
\right] = P^{-1}X \nonumber
\end{eqnarray}
結果、以下の独立した2個の常微分方程式が得られます。
\begin{eqnarray}
\frac{d}{dt}z_1 = \lambda_1 z_1 + b_1 \nonumber\\
\frac{d}{dt}z_2 = \lambda_1 z_2 + b_2
\label{eq:SimulEquation}
\end{eqnarray}
\begin{equation}
\hspace{30mm}
\left[ \begin{array}{c}
b_1 \\
b_2 \\
\end{array}\right]
:= P^{-1}Bf \nonumber
\end{equation}
つまり、式(\ref{eq:StateEquation})を計算するとは、式(\ref{eq:SimulEquation})の連立方程式を同時に計算するという事なのです。
\(c=1、c=2、c=5\) 及び\(c=6\)とダンピング係数を変化させたときの固有値\(\lambda\)を計算し、hを乗じた値をプロットすると、図3になります。
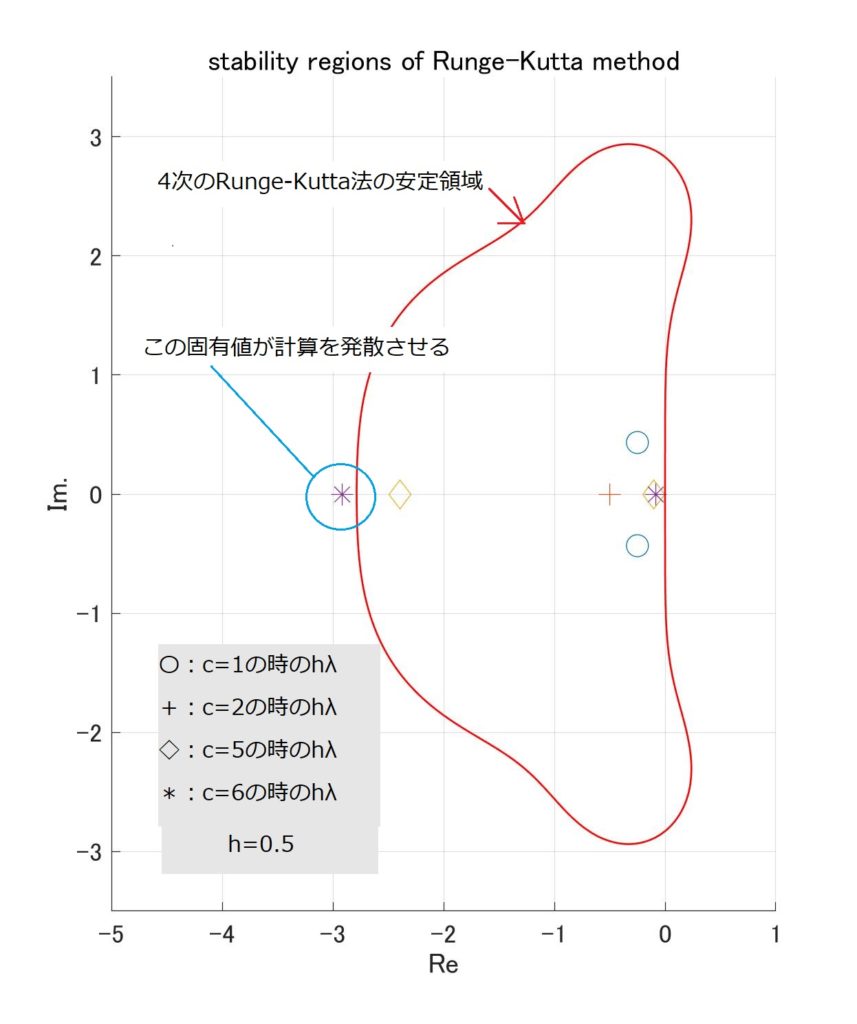
図3 ダンピング係数\(c\)と固有値の関係
「〇」でプロットしたのがc=1のときの固有値ですが、c=2で実軸上の「+」でプロットした場所に固有値(この場合は重根)が移動し、その後は実軸の上を原点に近い方向と、原点から遠い方向に分離していきます。
そしてダンピング係数\(c\)をたかだか6倍した程度で、「広くなって安心ね」の4次のRunge-kutta法の安定領域を超えていきます。
このように、原点に近い(遅い)固有値と、原点から遠い(速い)固有値を併せ持つ方程式をStiffな(=硬い)方程式と呼びます。運動方程式を構成したとき、”硬い”機械系をモデル化したときに発生した事が由来とされています[2]この”硬い”方程式が、ここでの例の様にダンピング過剰なのか、バネ定数が大きすぎたのかはわかりません。どなたかご存知でしょうか?。
Stiffな方程式の場合、原点から遠い固有値も安定領域に入るようにステップサイズを選ばなければなりませんが、それは、緩やかな(鈍い)運動を与えている原点に近い固有値に対しては、小さすぎることにもなりかねません
実務では、ダンピング力が速度に応じて変わるような非線形特性を組込みことがありますが、摩擦力を模擬するために、速度\(=0\)付近ではダンピング係数を大きく取る等のモデルを作ると、そこで計算が発散して一歩も先に進めない、というのはシミュレーションあるあるのネタ。
そうなると、ステップサイズ\(h\)を極端に小さくする意外に手がなくなり、計算時間がやたらと長くなります[3] … Continue reading。
「計算に時間がかかるから、その間は休憩」、なんてやっている部下をお持ちの方、それは計算の仕方が悪いんですよ。
ということで、次回は「4:Stiff対応の数値解法」です。
