Stiffな常微分方程式を計算するのは容易ではない。
これが前回の結論ですが、出来ないわけではない。いやStiff専用の数値解法が存在します。
\begin{equation}
\frac{dx(t)}{dt} = \lambda x(t)
\label{eq:scalar}
\end{equation}
という常微分方程式を
\begin{equation}
\frac{dx}{dt} \simeq \frac{x_{i+1}-x_i}{h} =\lambda x_i \\
\hspace{30mm} x_i=x(t_0) \quad x_{i+1}=x(t_0 +h)
\end{equation}
とするのが前進Euler法でしたが、
\begin{equation}
\frac{dx}{dt} \simeq \frac{x_{i}-x_{i-1} } {h} =\lambda x_i \\
\hspace{30mm} x_i=x(t_0) \quad x_{i-1}=x(t_0 – h)
\end{equation}
というのもアリなんじゃないか?という疑問が生じます。
これが後退Euler法です。
式を変形すると、その差が解りやすくなります。前進Euler法は
\begin{equation}
x_{i+1}=x_i + h\lambda x_i
\label{eq:FEequation}
\end{equation}
ですが、後退Euler法は
\begin{equation}
x_{i+1}=x_i + h\lambda x_{i+1}
\label{eq:BEequation}
\end{equation}
です。
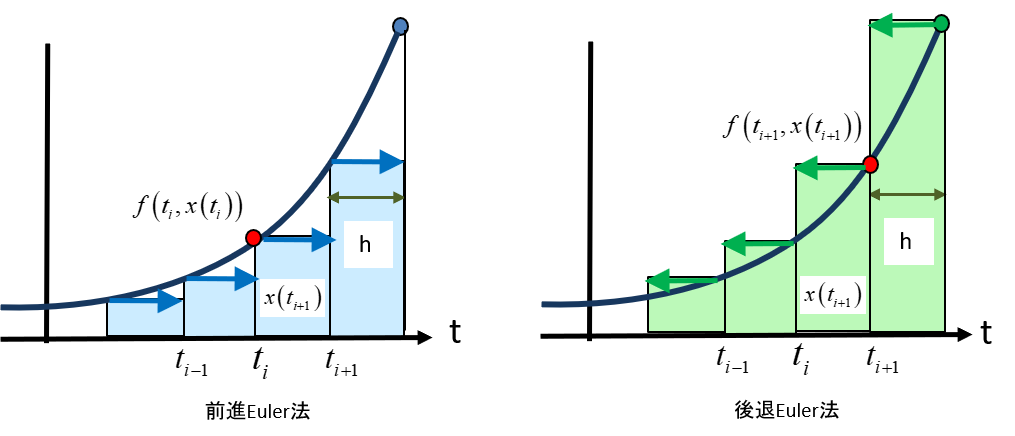
図1 後退Euler法と前進Euler法の違い
式\eqref{eq:FEequation}と式\eqref{eq:BEequation}の差は微妙ですが、その意味するところは図1のようになります。
そしてこの微妙な差は、計算安定領域に決定的な差を生じます。
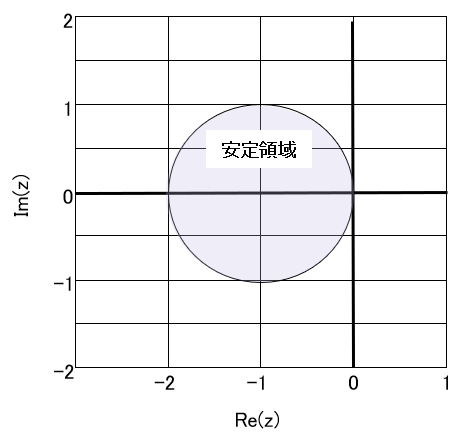
つまり、前進Euler法の安定領域は、
\begin{equation}
|1+h\lambda|<1
\label{eq:FEStableCond}
\end{equation}
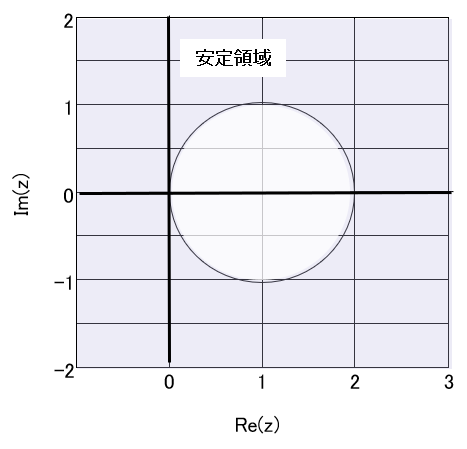
ですが、後退Euler法の安定領域は
\begin{equation}
\frac{1}{|1-h\lambda|}<1
\label{eq:BEStableCond}
\end{equation}
となり、左半平面が完全に含まれます。なお、このような特性をA安定(A-Stable)と言います。
つまり、連続系の式\eqref{eq:scalar}が発散しないなら、式\eqref{eq:BEequation}の後退Euler法も”絶対に”発散しないので、Stiffだろうが、固有値が遥か彼方だろうが、安定に計算することができます。
ですが、これで解決なんでしょうか?
まず、後退Euler法の問題点として、式\eqref{eq:BEequation}をよく見ると、左辺の\(x_{i+1}\)を得るために右辺の\(x_{i+1}\)を必要とします。穏やかでないですね。
このような方程式をImplicit-Method(陰解法)と言い、単純に右から計算して左に代入というわけにはいきませんから、適当な初期値を\(x_{i+1}\)に与え、少しずつ値を追い込んでいく、ニュートン法に代表される収束計算が必要となります [1]この例のような線形方程式の場合は、左辺へ移行して、除算または逆行列で計算できますが。
これに対して前進Euler法のような\(x_{i+1}\)を得るには\(x_{i}\)しか必要としない手法はexplicit-Method(陽解法)と呼ばれ、右から左へチャンチャンと計算できます。
後退Euler法のもう一つの問題点として、近似精度が1次であり4次のRunge-Kutta法などに比べ、計算精度が大幅に見劣りするという事があります。
状態方程式
\begin{equation}
\frac{dX}{dt}=AX+Bf \\
\label{eq:StateEquation}
\end{equation}
\begin{eqnarray}
\hspace{50mm}
X= \left[
\begin{array}{c}
v \\
y \\
\end{array}
\right]
\quad
A= \left[
\begin{array}{cc}
-c & -k \\
1 & 0 \\
\end{array}
\right]
\quad
B= \left[
\begin{array}{c}
9.8 \\
0 \\
\end{array}
\right] \nonumber
\end{eqnarray}
において、\(m=1 k=1 c=1\)を\(h=1\)で計算すると、
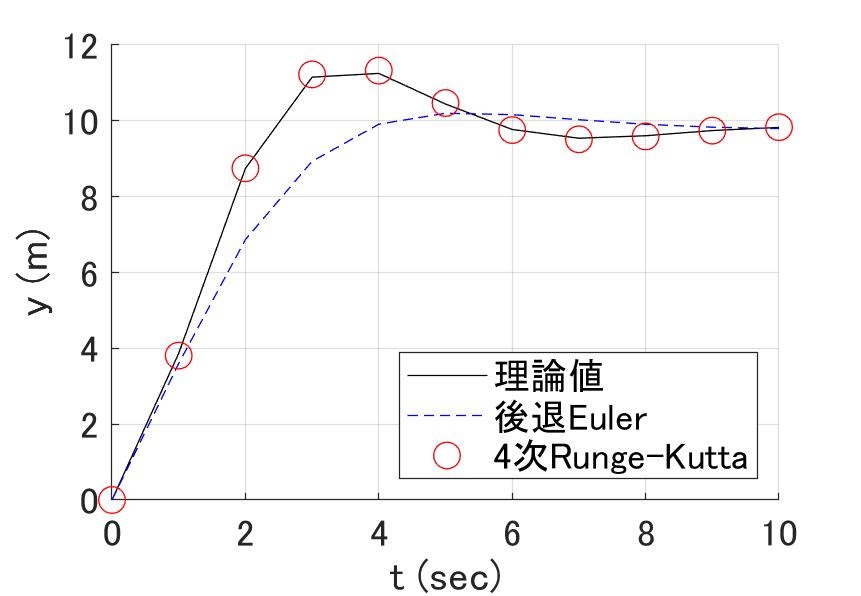
図4 4次のRunge-Kutta法と後退Euler法の$h=1$における計算結果
\(h=1\)というかなり大きめの計算ステップであっても、4次のRunge-Kutta法なら、ほぼ理論値ですが、後退Euler法は、”しかたねぇか”、という感じになります。
そこで、もう一度図1をじ~っと見ると、前進Euler法と後退Euler法を足して2で割ると、いい感じじゃね? という事に気付きます。
そこで、
\begin{equation}
2x_{i+1}=2x_i + h\lambda x_i + h\lambda x_{i+1}
\end{equation}
これを変形して、
\begin{eqnarray}
2x_{i+1}-h\lambda x_{i+1}=2x_i + h\lambda x_i \nonumber\\
x_{i+1} = \frac{2+h\lambda }{2-h\lambda} x_{i}
\end{eqnarray}
この手法は、台形積分法(Trapezoidal-Rule)と呼ばれます[2] … Continue reading。
安定領域は
\begin{equation}
\left| \frac{2+h\lambda }{2-h\lambda} \right|<1
\end{equation}
となり、これを図示すると、
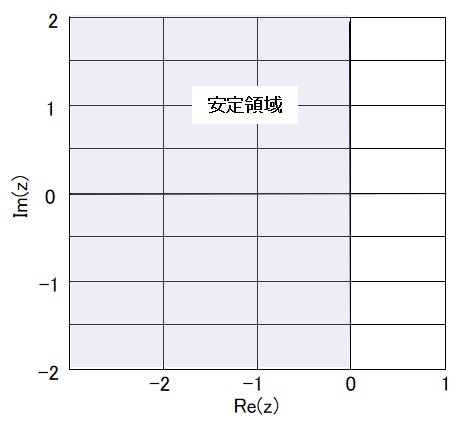
図5 台形積分法の安定領域
なので、「Oh! ぴったり左半平面!」 必要にして十分とはまさこの事、と狂喜します。
さらに、その計算精度は\(h\)の2次とされており、時系列で計算してみると、
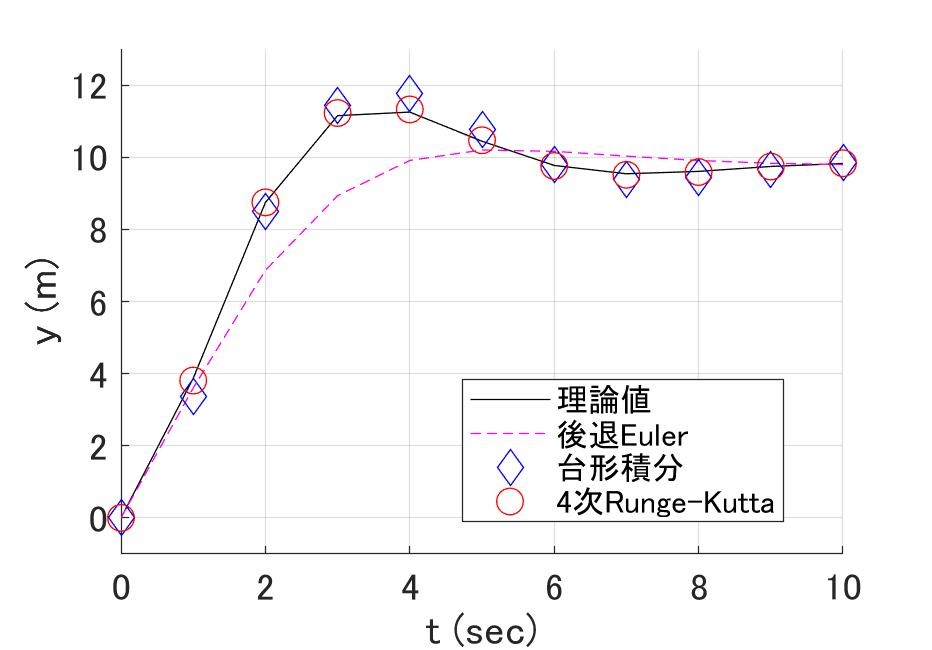
図6 4次のRunge-Kutta法と台形積分法の\(h=1\)における計算結果
かくして安定領域は必要にして十分、計算精度もそこそこある、ということで、Stiffな方程式に対する、有力な計算手法が得られました[3]「いや俺はGear法を信じる」、という方もいるでしょう。この件も後でキッチリオトシマエを付けます。
ですが、ここで終わればこのホームページを作ろうとは思わなかったわけで、やはり問題があるのですよ。
台形積分法もImplicitなので、計算するのはやっかいなのですが、それ以上にImplicit-Method全般に言えるような、問題というか、イチャモンがあると思っています。
ですが、その前に、前進/後退Euler法は1次、台形積分法は2次の精度とは何でしょうか?
まずは、その点を明らかにしておきましょう。
参考文献
「常微分方程式と微分方程式の数値解法」 U.M. アッシャー,L.R.ペツォルド 共著,中村 眞理雄 監訳 嘉村友作・三ツ間 均 共訳 2006年 培風館
「微分方程式による計算科学入門」 三井 斌友 小藤 俊幸 斉藤 善弘 2004年共立出版